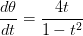直角三角形有长边而且它们的长度都随时间增加，这样:

求出角度的速率相反随时间变化。

a)首先，我们需要写一个角度的表达式作为函数．因为这个角是对边我们知道tan很简单．求正切的倒数:

现在我们需要求导．

回想一下反正切函数的一般导数是:

把这个应用到for函数上，记住使用链式法则，得到:

为了确定球形气泡表面积的变化率，我们必须把它和我们已知的东西联系起来体积的变化率。

球体的体积由以下公式给出:

体积的变化率由对时间的导数给出:

用以下规则求导数:

，

我们现在必须解出在指定半径处的半径变化率，以便稍后可以解出表面积变化率:

接下来，我们必须求出球面的表面积和表面积变化率，方法与上面相同:

把已知的表面积变化率代入到指定半径上，把这个半径代入到表面积变化率函数中，我们得到

为了求出直径的变化率，我们必须把直径和我们已知的物体的变化率联系起来:表面积。

披萨面团顶部的表面积由

变化率可以通过对函数对时间求导得到:

求出半径在给定半径处的变化率，我们得到

英寸/秒

现在，我们将直径与披萨面团的半径联系起来:

对两边对时间求导，得到

代入已知的半径变化率在给定半径处，我们得到

英寸/秒

我们可以直接用直径来表示表面积公式，但是我们使用的方法更适用于相关变化率不那么容易处理的问题。

为了确定圆周在给定半径处的变化率，我们必须将圆周变化率与我们已知的体积变化率联系起来。

从球形气球的体积方程开始，

我们求函数对时间的导数，得到体积的变化率:

用以下规则求导数:

，

我们用链式法则求半径对时间的导数，因为我们知道它是时间的函数。

解利用我们已知的在给定的半径下，我们得到

现在，我们把这个变化率应用到周长的变化率上，我们通过对周长对时间求导得到:

通过代入已知的半径变化率来求解周长的变化率，我们得到

为了求出给定直角三角形底对边的夹角变化率，当三角形是一定面积时，我们必须把它与三角形底的变化率联系起来。

首先，我们必须确定直角三角形的底边在给定区域的长度:

现在，我们必须找出底的对角与底的长度和高度的关系，即角的正切:

为了求出角度的变化率，我们对两边对时间求导，记住三角形的底与时间有关，而高度是常数:

我们知道底边的变化率，我们可以从三角形的边求出夹角:

把这个和其他已知的信息代入解出与底相邻角的变化率，我们得到

弧度/分钟

求加速度，求二阶导．

,

．

汽车的位置在然后由:

这是一个相关的利率问题。

因为题目给出了一个轨道的时间，我们可以求出这个点的角速度。角速度就是粒子在一秒内运动的弧度。我们把一圈的弧度除以，它转一圈的时间是8秒。

这就得到了角度随时间的变化量，．

现在我们需要把角度的位置，．回想一下,

，其中r为半径。

由于半径是一个单位，我们可以把这个方程写成

．

现在对两边求导时间，使用隐式微分。记住，对于任何不存在的变量，我们都使用链式法则．这给了,

．

现在我们有了一个公式，它与粒子在某一时刻的水平速度有关，，到x轴正上方的角度和角速度在同一时刻。我们要求求出x坐标变化的速度当的角度,是x轴正上方的弧度。我们代入为．然而，我们也需要知道．幸运的是，我们已经找到了。它是角速度，弧度/秒。

代入这个信息，我们得到

这就是答案。负号是有意义的，因为这个点是逆时针运动的。因此，当角度为时，它向左移动弧度。

这是一个相关的利率问题。梯子靠在建筑物的一侧形成一个直角三角形，10英尺的梯子是它的斜边。勾股定理，把这个三角形的三条边联系起来。让从梯子顶端到地面的高度。让是从梯子底部到建筑物的距离。因为10是斜边，我们有下面的等式。

把右边化简得到

自而且都是变量，我们要在求导之后再代入值。

问题是，站在梯子顶端的人下落的速度有多快当梯子的底部距离建筑物6英尺，并以2英尺/秒的速度滑动。这两个值，而且，只发生在某一瞬间。我们要求出方程在这个时间点的导数。

用隐微分求对时间的导数，我们得到

我们只关心那一瞬间而且．我们需要找出梯子顶端，也就是这个人，下降的速率。我们要解出．然而，我们需要知道是什么就是在这一瞬间，为了找到一个答案。幸运的是，勾股定理适用于所有时间点，所以我们可以用它来求这个特定的时刻．

因为我们处理的是物理距离，所以我们只用正8。

把所有的信息代入导数方程

负号是有道理的，因为人在往下掉，所以高度变小了。因此我们的答案是

为了求出行进的总距离，速度函数必须从来小时:

最后一个问题是，这辆车离家有多远。在离家三英里的地方，所以在，它将是:

离家很远。