All Calculus 3 Resources
Example Questions
Example Question #1 :Calculus 3
Suppose the vectors


Example Question #2 :Calculus 3
The vector-valued function


Find a tangent vector to

Example Question #2 :Calculus 3
Let
Find
Example Question #4 :Calculus 3
Let
Find its linear approximation at
Hint: Use Taylor's formula.
Example Question #3 :Calculus 3
Let

Notice that




First, we need to find

Then, we need to find
The answer is
Example Question #1 :Numerical Approximations To Definite Integrals
Evaluate:
cannot be determined
First, we can write out the first few terms of the sequence

Notice that each term







The answer is
Example Question #3 :Calculus 3
Find

We will have to find the first derivative of




We will apply the chain rule on the left side.
We now solve for the first derivative with respect to
In order to get the second derivative, we will differentiate

We will replace

But, from the original equation,


The answer is
Example Question #1 :Calculus 3
Which of the following represents the graph of the polar function
First, mulitply both sides by r.
Then, use the identities

The answer is
Example Question #1 :Calculus 3
We can use the substitution technique to evaluate this integral.
Let
We will differentiate



We can solve for


We will also need to change the bounds of the integral. When



We will now substitute



The answer is
Example Question #3 :Calculus 3
Evaluate the following limit:
Does not exist.
First, let's multiply the numerator and denominator of the fraction in the limit by
As




The answer is
Certified Tutor
Certified Tutor
All Calculus 3 Resources





























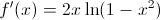




















![\frac{d}{dx}[y^2-x^2]=\frac{d}{dx}[4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24767/gif.latex)
![\frac{d}{dx}[y^2]\cdot \frac{dy}{dx}-\frac{d}{dx}[x^2]=0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24768/gif.latex)


![\frac{d}{dx}\frac{dy}{dx}=\frac{d^{2}y}{dx^{2}}=\frac{d}{dx}[\frac{x}{y}]=\frac{y\cdot \frac{d}{dx}[x]-x\cdot \frac{d}{dx}[y]}{y^{2}} =\frac{y\cdot 1-x\cdot \frac{dy}{dx}}{y^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24772/gif.latex)
































