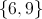We can draw a Venn diagram of these students.

Drawn this way, there are more students on the Venn diagram than we have.

This is because some of the students play both sports and should be in the overlap on the Venn diagram. To find the number of students in the overlap, subtract the total number of students given from the number on the diagram.

This represents the number of students who were counted twice, or the number in the overlap.

We can redraw the correct Venn diagram with this number.

The notationstands for "A union C," which refers to everything that is in either setor set.

When we add the numbers together, we get:

A Venn diagram can help us determine the total number of students in the class.

First, we must calculate the number of students who have ONLY cats or ONLY dogs. First, for cats, 15 students have cats, and 5 students have both cats and dogs.

Ten students have only cats.

For dogs, 12 students have dogs, and 5 students have both cats and dogs.

Seven students have only dogs.

Using this information, we can fill in the Venn diagram.

This diagram shows the 10 students with only cats, the 7 students with only dogs, the 5 students with both, and the 8 students with neither. Adding up the numbers will give us the total number of students.

represents the union of the two sets. The union of Sets A and B is the set of elements which appear in A, in B, or in both A and B.

Therefore,

The formula for intersection isP(aorb) =P(a) +P(b) –P(aandb).

Now, 30 students out of 100 swim, soP(swim) = 30/100 = 3/10.

40 students run out of 100, soP(run) = 40/100 = 4/10. Notice how we are keeping 10 as the common denominator even though we could simplify this further. Keeping all of the fractions similar will make the addition and subtraction easier later on.

Finally, 20 students swim AND run, soP(swim AND run) = 20/100 = 2/10. (Again, we keep this as 2/10 instead of 1/5 so that we can combine the three fractions more easily.)

P(swim OR run) =P(swim) +P(run) –P(swim and run)

= 3/10 + 4/10 – 2/10 = 5/10 = 1/2.

The intersection of two sets contains every element that is present in both sets, sois the correct answer.

The idea is to draw a Venn Diagram and find the intersection. We have one circle of 70 and another with 40. When we add the two circles plus the 10 students who joined neither, we should get 100 students. However, when adding the two circles, we are adding the intersections twice, therefore we need to subtract the intersection once.

We get, which means the intersection is 20.

Ifstudents are enrolled in sciences, but there are onlystudents then we must find how many overlap in the subjects they take.

To do this we can subtractfrom.

Therefore,of those "enrollments" must be doubles.

Thosestudents take both Chemistry and Biology.

画一个维恩图与三个子集:数学,合作伙伴nce, and English. Start in the center with students that like all three subjects. Next, look at students that liked two subjects. Be sure to subtract out the ones already counted in the middle. Then, look at the students that only like one subject. Be sure to subtract out the students already accounted for. Once all of the subsets are filled, look at those students who don’t like any of these subjects. To find the students who don’t like any of these subjects add all of the students who like at least one subject from the total number of students surveyed, which is 50.

M = math

S = science

E = English

M∩S∩E = 3

M∩S = 5 (but 3 are already accounted for) so 2 for M and S ONLY

M∩E = 7 (but 3 are already accounted for) so 4 for M and E ONLY

S∩E = 8 (but 3 are already accounted for) so 5 for S and E ONLY

M = 14 (but 3 + 2 + 4 are already accounted for) so 5 for M ONLY

S = 20 (but 3 + 2 + 5 are already accounted for) so 10 for S ONLY

E = 28 (but 3 + 4 + 5 are already accounted for) so 16 for E ONLY

Therefore, the students already accounted for is 3 + 2 +4 + 5 + 5 + 10 + 16 = 45 students

So, those students who don’t like any of these subjects are 50 – 45 = 5 students

A = {2, 4, 6, 8, 10, 12}

B = {3, 6, 9, 12, 15, 18}

The intersection of a set means that the elements are in both sets: A∩B = {6, 12}