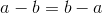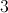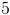An even number subtracted from an odd number will always produce an odd result.

None of the other answer choices are correct.

Pick any even integer (2, 4, 6, etc.) to representx．唯一的价值是奇怪的是3x+ 1. Any number multiplied by an even integer will be even. When an even number is added and subtracted to that product, the result will be even as well. 3x+ 1是唯一的选择,增加了一个奇数the product.

While I & II can be true, examples can be found that show they are not always true (for example, 2²/2²is odd and 4²/2²is even).

III is always true – a square even number is always divisible by four, and the distributive property tell us that adding two numbers with a common factor gives a sum that also has that factor.

Sconsists of all even integers. If we were to increase each of these even numbers by 2, then we would get another set of even numbers, because adding 2 to an even number yields an even number. In other words,Talso consists entirely of even numbers.

In order to find the mean ofT, we would need to add up all of the elements inTand then divide by however many numbers are inT．If we were to add up all of the elements ofT, we would get an even number, because adding even numbers always gives another even number. However, even though the sum of the elements inTmust be even, if the number of elements inTwas an even number, it's possible that dividing the sum by the number of elements ofTwould be an odd number.

For example, let's assumeTconsists of the numbers 2, 4, 6, and 8. If we were to add up all of the elements ofT, we would get 20. We would then divide this by the number of elements inT, which in this case is 4. The mean ofTwould thus be 20/4 = 5, which is an odd number. Therefore, the mean ofTdoesn't have to be an even number.

Next, let's analyze the median ofT．Again, let's pretend thatTconsists of an even number of integers. In this case, we would need to find the average of the middle two numbers, which means we would add the two numbers, which gives us an even number, and then we would divide by two, which is another even number. The average of two even numbers doesn't have to be an even number, because dividing an even number by an even number can produce an odd number.

For example, let's pretendTconsists of the numbers 2, 4, 6, and 8. The median ofTwould thus be the average of 4 and 6. The average of 4 and 6 is (4+6)/2 = 5, which is an odd number. Therefore, the median ofTdoesn't have to be an even number.

Finally, let's examine the range ofT．The range is the difference between the smallest and the largest numbers inT, which both must be even. If we subtract an even number from another even number, we will always get an even number. Thus, the range ofTmust be an even number.

Of choices I, II, and III, only III must be true.

The answer is III only.

I)xy is Even*Odd is Even. II) x-y is Even+/-Odd is Odd. III) 3x is Odd*Even =Even, 2y is Even*Odd=Even, Even + Even = Even. Therefore only II is Odd.

I. xyz = even * odd * even = even

II. 2x + 3y = even*even + odd*odd = even + odd = odd

III. z²– y = even * even – odd = even – odd = odd

Therefore only I will give an even number.

Since we are only told that "at least" one of the numbers is even, we could have one even and one odd integer OR we could have two even integers.

Even plus odd is odd, but even plus even is even, sox+ycould be either even or odd.

Even times odd is even, and even times even is even, soxymust be even.

In order to solve this problem, it will help us to find all of the possible scenarios ofa,b,a², andb²．We need to make use of the following rules:

1. The product of two even numbers is an even number.

2. The product of two odd numbers is an odd number.

3. The product of an even and an odd number is an even number.

The information that we are given is thatab²is an even number. Let's think ofab²as the product of two integers:aandb²．

In order for the product ofaandb²to be even, at least one of them must be even, according to the rules that we discussed above. Thus, the following scenarios are possible:

Scenario 1:ais even andb²is even

Scenario 2:ais even andb²is odd

Scenario 3:ais odd andb²is even

Next, let's consider what possible values are possible forb．Ifb²is even, then this meansbmust be even, because the product of two even numbers is even. Ifbwere odd, then we would have the product of two odd numbers, which would mean thatb²would be odd. Thus, ifb²is even, thenbmust be even, and ifb²is odd, thenbmust be odd. Let's add this information to the possible scenarios:

Scenario 1:ais even,b²is even, andbis even

Scenario 2:ais even,b²is odd, andbis odd

Scenario 3:ais odd,b²is even, andbis even

Lastly, let's see what is possible fora²．Ifais even, thena²must be even, and ifais odd, thena²must also be odd. We can add this information to the three possible scenarios:

Scenario 1:ais even,b²is even, andbis even, anda²is even

Scenario 2:ais even,b²is odd, andbis odd, anda²is even

Scenario 3:ais odd,b²is even, andbis even, anda²is odd

Now, we can use this information to examine choices I, II, and III.

Choice I asks us to determine ifa²must be even. If we look at the third scenario, in whichais odd, we see thata²would also have to be odd. Thus it is possible fora²to be odd.

Next, we can analyzea²b．In the first scenario, we see thata²is even andbis even. This means thata²bwould be even. In the second scenario, we see thata²is even, andbis odd, which would still mean thata²bis even. And in the third scenario,a²is odd andbis even, which also means thata²bwould be even. In short,a²bis even in each of the possible scenarios, so it must always be even. Thus, choice II must be true.

We can now look atab．In scenario 1,ais even andbis even, which means thatabwould also be even. In scenario2,ais even andbis odd, which means thatabis even again. And in scenario 3,ais odd andbis even, which again means thatabis even. Therefore,abmust be even, and choice III must be true.

The answer is II and III only.

The word "product" refers to the answer of a multiplication problem. Since 2 times 8 equals 16, it is a valid pair of numbers.

Ifis an odd integer then we can plug 1 intoand solve foryielding 13. 13 is prime, meaning it is only divisible by 1 and itself.