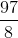我们周六和周日开放!

现在打电话设置辅导:

(888) 888 - 0446

微分方程:常微分方程的数值解

学习微分方程的概念，示例问题和解释

创建帐户创建测试和抽认卡

所有微分方程资源

1诊断测试 29练习题今日问题抽认卡概念学习

例子问题

问题1:常微分方程的数值解

用欧拉法计算近似值 y(0.2) 在哪里 y(x) 是下式初值问题的解。

y''+xy'+y=0

y(0)=2, y'(0)=3

可能的答案:

$y(0.2)\approx2.58$

$y(0.2)\approx2.458$

$y(0.2)\approx2.542$

$y(0.2)\approx2.5$

$y(0.2)\approx2.584$

正确答案:

$y(0.2)\approx2.58$

解释：

用欧拉法求函数

y''+xy'+y=0

y(0)=2, y'(0)=3

首先代入

$\\y'=u \\u'=-xu-y$

因此

$\\y_{n+1}=y_n+hu_n \\u_{n+1}=u_n+h[-x_nu_n-y_n]$

在哪里表示步长。

让

$\\h=0.1 \\y_0=2 \\u_0=3$

将这些值代入前面的公式中，并以这种方式继续下去，直到得到的近似值 y(0.2) 是发现。

$\\y_1=y_0+(0.1)u_0=2+(0.1)(3)=2.3 \\u_1=u_0+(0.1)[-x_0u_0-y_0]=3+(0.1)[0(2)-2]=2.8 \\y_2=y_1+(0.1)u_1=2.3+(0.1)(2.8)=2.58 \\u_2=u_1+(0.1)[-x_1u_1-y_1]=2.8+(0.1)[-0.1(2.8)-2.3]=2.542$

因此,

$y(0.2)\approx2.58$

报告错误

问题51:微分方程

近似 $y(\pi)$ 为 $y = \cos(y)(2-y)$ 有时间步长 $h = \frac{\pi}{4}$ 和 y(0) = 0 。

可能的答案:

$\frac{3\pi}{2}$

$\frac{\pi}{2}$

$\frac{\pi}{4}$

$\frac{5\pi}{8}$

正确答案:

$\frac{\pi}{2}$

解释：

近似 $y(\pi)$ 为 $y = \cos(y)(2-y)$ 有时间步长 $h = \frac{\pi}{4}$ 和 y(0) = 0 。

欧拉近似的公式 $\mu(t+h) = \mu (t) + h \cdot f(t, \mu(t))$ 。

插入，我们有

$\mu(\frac{\pi}{4}) = \mu (0) + \frac{\pi}{4}f(0, \mu(0)) = 0 + \frac{\pi}{4}(\cos(0)(2-0)) = \frac{\pi}{2}$

$\mu(\frac{\pi}{2}) = \mu (\frac{\pi}{4}) + \frac{\pi}{4}f(\frac{\pi}{4}, \mu(\frac{\pi}{4})) = \frac{\pi}{2} + \frac{\pi}{4}(\cos(\frac{\pi}{2})(2-\frac{\pi}{2})) = \frac{\pi}{2} + 0 = \frac{\pi}{2}$

在这里，我们可以看到我们被困在水平切线上(当使用较大的时间步长时，欧拉方法的失败)。由于函数不依赖于t，我们将继续在水平线上移动剩下的欧拉近似。因此 $\mu(\pi) = \frac{\pi}{2} \approx y(\pi)$ 。

报告错误

问题1:常微分方程的数值解

用欧拉法计算近似值 y(0.2) 在哪里 y(x) 是下式初值问题的解。

y''+xy'+y=0

y(0)=2, y'(0)=3

可能的答案:

$y(0.2)\approx2.5$

$y(0.2)\approx2.58$

$y(0.2)\approx2.542$

$y(0.2)\approx2.458$

$y(0.2)\approx2.584$

正确答案:

$y(0.2)\approx2.58$

解释：

用欧拉法求函数

y''+xy'+y=0

y(0)=2, y'(0)=3

首先代入

$\\y'=u \\u'=-xu-y$

因此

$\\y_{n+1}=y_n+hu_n \\u_{n+1}=u_n+h[-x_nu_n-y_n]$

在哪里表示步长。

让

$\\h=0.1 \\y_0=2 \\u_0=3$

将这些值代入前面的公式中，并以这种方式继续下去，直到得到的近似值 y(0.2) 是发现。

$\\y_1=y_0+(0.1)u_0=2+(0.1)(3)=2.3 \\u_1=u_0+(0.1)[-x_0u_0-y_0]=3+(0.1)[0(2)-2]=2.8 \\y_2=y_1+(0.1)u_1=2.3+(0.1)(2.8)=2.58 \\u_2=u_1+(0.1)[-x_1u_1-y_1]=2.8+(0.1)[-0.1(2.8)-2.3]=2.542$

因此,

$y(0.2)\approx2.58$

报告错误

问题1:常微分方程的数值解

使用隐式的用欧拉法近似 y(3) 为 y' = 5y ，考虑到 y(0) = 4 ，使用时间步长为 h = 1.

可能的答案:

$\frac{1}{32}$

$-\frac{1}{16}$

$\frac{1}{16}$

正确答案:

$-\frac{1}{16}$

解释：

在隐式方法中，增加的量由 $h \cdot f(t_{i+1}, y_{i+1})$ 在这种情况下 $\mu_i = \mu_{i-1}+ 1 \cdot (5\mu_i)$ 。注意，你不能直接代入这种形式的方程，因为它是隐式的 $\mu_i$ 是在两边。值得庆幸的是，这是一个非常简单的形式，您可以显式地求解。否则，你就得用近似法比如牛顿法来求 $\mu_i$ 。明确地求解，我们有 $-4\mu_i = \mu_{i-1}$ 和 $\mu_i = -\frac{\mu_{i-1}}{4}$ 。

因此, $y(1) \approx \mu_1 = -\frac{4}{4} = -1$

$y(2) \approx \mu_2 = -\frac{-1}{4} = \frac{1}{4}$

$y(3) \approx \mu_3 = -\frac{\frac{1}{4}}{4} = -\frac{1}{16}$

这样，我们就得到了最后的答案 $-\frac{1}{16}$

报告错误

问题1:欧拉方法

用欧拉法的两个步骤 h=0.1 在

$y' = x\sqrt{y} \ \ \ y(1) = 4$

到小数点后三位

可能的答案:

4.428

4.420

4.408

4.413

4.425

正确答案:

4.425

解释：

欧拉法告诉我们

$y_{n+1} = y_n + hf(x_n,y_n) = y_n + (0.1)x_n\sqrt{y_n}$

迈出一步

$y_1 = y_0 + (0.1)x_0\sqrt{y_0} = 4 + (0.1)(1)\sqrt{4} = 4.2$

再走一步

$y_2 = y_1 + (0.1)x_1\sqrt{y_1} = 4.2 + (0.1)(1.1)\sqrt{4.2} \approx 4.425$

报告错误

问题1:常微分方程的数值解

Adams-Bashforth两步逼近法采用近似格式 $y_{i+2} = y_{i+1} - \frac{1}{2}hf(t_i, y_i) + \frac{3}{2}hf(t_{i+1}, y_{i+1})$ 。

考虑到 y(0) = 1 和 y(1) = 2 ，使用Adams-Bashforth方法进行近似 y(3) 为 y = -y^2 步长为 h = 1.

可能的答案:

$\frac{33}{4}$

$\frac{133}{8}$

$\frac{97}{8}$

$-\frac{159}{8}$

$\frac{55}{8}$

正确答案:

$-\frac{159}{8}$

解释：

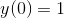
在这个问题中，我们有两个点，所以我们可以马上开始代入。如果不是，我们可以近似 $y_{i+1}$ 用显式欧拉法求解 $y_{i}$ 。

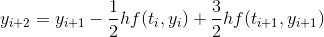
插进 $y_{i+2} = y_{i+1} - \frac{1}{2}hf(t_i, y_i) + \frac{3}{2}hf(t_{i+1}, y_{i+1})$ ，我们有

$y(2) \approx \mu_2 = 2 -\frac{1}{2}\cdot 1 \cdot -1^2 + \frac{3}{2}\cdot 1 \cdot -2^2 = 2 +\frac{1}{2} - 6 = -\frac{7}{2}$

$y(3)\approx \mu_3 = -\frac{7}{2} + \frac{1}{2}\cdot4 - \frac{3}{2}\cdot \frac{49}{4} =-\frac{159}{8}$ 。

注意，对于如此大的时间步长，我们的近似可能不是很好，但是无论精度如何，过程都不会改变。

$y(3)\approx -\frac{159}{8}$

报告错误

问题1:常微分方程的数值解

求二阶边值问题的解。 y'' -2y' + 2y = 0 ， y(0) = 0 ， $y\left(\frac{\pi}{2}\right) = 1$ 。

可能的答案:

$y = 10e^{2t}\sin(2t)$

$y = e^{t}\sin(t) - e^t\cos(t)$

$y = e^{t -\frac{\pi}{2}}\sin(t)$

边值问题没有解。

$y = 5e^t\sin(t) + 3e^t\cos(t)$

正确答案:

$y = e^{t -\frac{\pi}{2}}\sin(t)$

解释：

的特征方程 y'' -2y' + 2y = 0 是 $\lambda^2 - 2\lambda + 2 = 0$ ，解为 $\frac{2 \pm \sqrt{4 - 8}}{2} = 1 \pm i$ 。因此，齐次问题的通解为 $y = c_1e^t\sin(t) + c_2e^t\cos(t)$ 。代入条件，我们得到 y(0) = c_2 = 0 ，所以 $y = c_1e^t\sin(t)$ 。代入第二个条件，我们得到 $y\left(\frac{\pi}{2}\right) = c_1e^{\frac{\pi}{2}} = 1$ 这 $c_1 = e^{-\frac{\pi}{2}}$ 。

因此，最终的解决方案是 $y = e^{t -\frac{\pi}{2}}\sin(t)$ 。

报告错误

问题1:常微分方程的数值解

求二阶边值问题的解。 y'' + 9y = 0 ， y(0) = 0 ， $y\left(2\pi\right) = 1$ 。

可能的答案:

$y = 3\sin(3t)$

$y = 3\cos(3t)$

边值问题没有解。

$y = \sin(3t) + 2 \cos(3t)$

$y = 4\sin(3t) - \cos(3t)$

正确答案:

边值问题没有解。

解释：

的特征方程 y'' + 9y = 0 是 $\lambda^2 + 9 = 0$ 解为 $\pm 3i$ 。这告诉我们齐次方程的解是 $y = c_1\sin(3t) + c_2\cos(3t)$ 。代入条件，我们得到 y(0) = c_2 = 0 如此......以至于...... $y = c_1\sin(3t)$ 。代入第二个条件，我们有 $y(2\pi) = 0 = 1$ 这显然是错误的。

这个问题证明了初值问题和边值问题的重要区别:边值问题并不总是有解。这是我们找不到的一个这样的例子 c_1, c_2 满足我们的条件。

报告错误

查看微分方程导师

杰克
认证导师

中国科学技术大学，理学学士，数学。特拉华大学，数学哲学博士。

查看微分方程导师

马利克
认证导师

东北大学物理系理学学士。

查看微分方程导师

旧金山
认证导师

德克萨斯大学布朗斯维尔分校，数学学士。德克萨斯大学布朗斯维尔分校，数学硕士。

所有微分方程资源

1诊断测试 29练习题今日问题抽认卡概念学习

受欢迎的科目

费城的GRE导师，旧金山湾区的微积分导师，凤凰城西班牙语家教，西雅图的SSAT导师，芝加哥西班牙语家教，休斯顿的计算机科学导师，休斯顿的西班牙语家教，达拉斯沃斯堡的法语家教，华盛顿特区的SAT辅导老师，MCAT在纽约市的导师

流行备考

LSAT考试准备在休斯敦，SAT考试准备在休斯敦，在凤凰城SAT考试准备，芝加哥LSAT考试准备，西雅图MCAT考试准备，洛杉矶的LSAT考试准备，芝加哥GMAT考试准备，SAT考试准备在西雅图，在旧金山湾区的ACT考试准备，纽约市的ISEE考试准备

DMCA的抱怨

如果您认为通过本网站提供的内容(定义见我们的服务条款)侵犯了您的一项或多项版权，请向下列指定代理提供包含以下信息的书面通知(“侵权通知”)。如果Varsity Tutors针对侵权通知采取行动，则将善意地尝试通过该方提供给Varsity Tutors的最新电子邮件地址(如果有的话)联系提供此类内容的一方。

您的侵权通知可能会转发给提供内容的一方或第三方，如ChillingEffects.org。

请注意，如果您对产品或活动侵犯了您的版权做出重大虚假陈述，您将承担损害赔偿责任(包括成本和律师费)。因此，如果您不确定网站上的内容或链接的内容侵犯了您的版权，您应该首先考虑联系律师。

请按照以下步骤提交通知:

你必须包括以下内容:

版权所有人或被授权代表其行事的人的物理或电子签名;对被主张侵犯的版权的认定;对您声称侵犯您版权的内容的性质和确切位置的描述，并提供足够的细节，以便大学导师能够找到并积极识别该内容;例如，我们需要一个特定问题的链接(不仅仅是问题的名称)，其中包含问题的内容和描述-图像，链接，文本等-您的投诉涉及的特定部分;您的姓名、地址、电话号码和电子邮件地址;您的声明:(A)您真诚地相信，使用您声称侵犯您版权的内容未经法律授权，或未经版权所有者或其代理人授权;(b)您的侵权通知中包含的所有信息都是准确的，并且(c)在伪证罪的处罚下，您是版权所有者或被授权代表其行事的人。

向我们的指定代理投诉:

Charles Cohn Varsity Tutors LLC
汉利路101号，300室
圣路易斯，密苏里州63105

或填写以下表格:

不填这个栏

联系信息

*法定全称

公司名称

*电话号码

*电子邮件地址

地址

*Address1

Address2

*城市

*状态

*Zipcode

*国家

投诉细节

你所代表的版权持有人(如果不是你本人)

*版权作品的URL(你的原始材料所在的位置)

*请说明受版权保护的作品，以便于辨认

我是据称受到侵犯的专有权的所有者，或被授权代表所有者行事的代理人。

这份通知是准确的。

我承认，使用此程序进行虚假或恶意的版权侵权指控可能会产生不利的法律后果。

*签名(您的数字签名具有法律约束力)

高中

研究生院

学习

搜索50+测试

数学辅导

科学辅导

外语

小学辅导

其他

搜索350+主题

微分方程:常微分方程的数值解

学习微分方程的概念，示例问题和解释

所有微分方程资源

例子问题

问题1:常微分方程的数值解

问题51:微分方程

问题1:常微分方程的数值解

问题1:常微分方程的数值解

问题1:欧拉方法

问题1:常微分方程的数值解

问题1:常微分方程的数值解

问题1:常微分方程的数值解

所有微分方程资源

报告与此问题相关的问题

DMCA的抱怨

联系信息

地址

投诉细节

寻找最好的导师

电子邮件地址:
你的名字:
反馈: