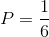例子问题
例子问题1:独立事件:Ccss.Math.Content.Hss Cp.A.2
明天下雨的可能性为25%。明天黄金价格上涨的概率是37%。明天下雨而金价上涨的概率是9.25%。这两个事件是独立的吗?
是的
没有
无法确定
是的
例子问题2:独立事件:Ccss.Math.Content.Hss Cp.A.2
汽车经销商负责汽车库存。他们决定注意停车场中汽车和卡车的数量,以及车辆的变速箱类型:自动还是手动。他们将这些数据输入到下面的表格中:

一个潜在的购车者想要购买一辆车,并询问车型是否独立于变速箱风格。根据数据,购买一辆卡车是否独立于拥有手动变速器?
为了解决与这个标准相关的问题,我们需要理解两个主要组成部分:概率和独立事件的性质。概率通常被定义为事件发生的机会或可能性。它是通过识别两个组件来计算的:事件和样本空间。事件被定义为我们希望看到的有利结果或成功。另一方面,样本空间被定义为事件所有可能结果的集合。在数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:掷骰子。我们想知道摇到1点的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
以分数形式表示的概率值将在0到1之间。1表示事件一定会发生,而0表示事件不会发生。同样,用百分比表示的概率值在0到100%之间,其中接近0的概率不太可能发生,接近100%的概率更有可能发生。
现在我们可以计算概率了,我们可以回顾一下独立事件的性质。独立事件的概率说明两个事件(A和B)是独立的,当且仅当事件A的概率乘以事件B的概率等于事件A和事件B的交集发生的概率。它可以写成如下表达式:
让我们回到骰子的例子。掷1对1骰子的概率和掷2骰子的概率是独立的吗?首先,让我们计算一下摇到1的概率。
现在,让我们求出在同一次骰子中另一个骰子掷到2的概率。
让我们把这两个概率相乘。
现在,让我们求出在两个不同的骰子上同时摇到1和2的概率。
让我们比较一下这两种可能性。
因此,概率是相等的,
让我们看另一个例子。一个人有一个装满10颗弹珠的袋子:6颗白色弹珠和4颗黑色弹珠。他想知道取出一颗白球的概率是否独立于取出一颗黑球的概率。让我们从计算取出一个黑色弹珠的概率开始。
现在让我们计算取出一个白色弹珠的概率。
让我们把这两个概率相乘。
现在让我们观察一下同时发生的这些事件。假设一个黑色的弹珠首先被从袋子里拿出来。黑色弹珠的概率如下:
这和以前一样;然而,取出白色弹珠的概率发生了变化,因为从袋子中取出了一颗弹珠。
两者发生的概率可以写成:
概率是不相等的。
这是因为这两个事件是相互依赖的。当一个弹珠在第一次抓取时被拉(无论它是黑的还是白的)并且没有被替换,在第二次抓取时被拉的弹珠总数是不同的。因此,从第一次事件到第二次事件,抽出特定颜色弹珠的概率发生了变化。这种情况可以通过使用两个具有相同大理石成分的独立袋子来实现,或者在第二次尝试拉另一个大理石之前,在它们被拉完后将它们替换掉。这些信息已经说明了独立性的性质,以及如何计算事件是否彼此独立。
现在,我们可以用这个信息来解决这个问题。问题要求我们确定购买卡车的概率是否与是否有手动变速箱无关。在这种情况下,我们需要调查下面的表达式是否正确:
首先,让我们计算一下在停车场找到卡车的相关概率。
现在让我们计算一下一辆车有手动档的概率。
现在,我们需要计算这两个事件同时发生的概率。
现在,让我们看看下面的表达式是否正确:
利用这些信息,我们知道正确答案如下:
例子问题3:独立事件:Ccss.Math.Content.Hss Cp.A.2
汽车经销商负责汽车库存。他们决定注意停车场中汽车和卡车的数量,以及车辆的变速箱类型:自动还是手动。他们将这些数据输入到下面的表格中:
一个潜在的购车者想要购买一辆车,并询问车型是否独立于变速箱风格。根据数据,购买一辆独立于它的汽车是否拥有自动变速器?
为了解决与这个标准相关的问题,我们需要理解两个主要组成部分:概率和独立事件的性质。概率通常被定义为事件发生的机会或可能性。它是通过识别两个组件来计算的:事件和样本空间。事件被定义为我们希望看到的有利结果或成功。另一方面,样本空间被定义为事件所有可能结果的集合。在数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:掷骰子。我们想知道摇到1点的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
以分数形式表示的概率值将在0到1之间。1表示事件一定会发生,而0表示事件不会发生。同样,用百分比表示的概率值在0到100%之间,其中接近0的概率不太可能发生,接近100%的概率更有可能发生。
现在我们可以计算概率了,我们可以回顾一下独立事件的性质。独立事件的概率说明两个事件(A和B)是独立的,当且仅当事件A的概率乘以事件B的概率等于事件A和事件B的交集发生的概率。它可以写成如下表达式:
让我们回到骰子的例子。掷1对1骰子的概率和掷2骰子的概率是独立的吗?首先,让我们计算一下摇到1的概率。
现在,让我们求出在同一次骰子中另一个骰子掷到2的概率。
让我们把这两个概率相乘。
现在,让我们求出在两个不同的骰子上同时摇到1和2的概率。
让我们比较一下这两种可能性。
因此,概率是相等的,
让我们看另一个例子。一个人有一个装满10颗弹珠的袋子:6颗白色弹珠和4颗黑色弹珠。他想知道取出一颗白球的概率是否独立于取出一颗黑球的概率。让我们从计算取出一个黑色弹珠的概率开始。
现在让我们计算取出一个白色弹珠的概率。
让我们把这两个概率相乘。
现在让我们观察一下同时发生的这些事件。假设一个黑色的弹珠首先被从袋子里拿出来。黑色弹珠的概率如下:
这和以前一样;然而,取出白色弹珠的概率发生了变化,因为从袋子中取出了一颗弹珠。
两者发生的概率可以写成:
概率是不相等的。
这是因为这两个事件是相互依赖的。当一个弹珠在第一次抓取时被拉(无论它是黑的还是白的)并且没有被替换,在第二次抓取时被拉的弹珠总数是不同的。因此,从第一次事件到第二次事件,抽出特定颜色弹珠的概率发生了变化。这种情况可以通过使用两个具有相同大理石成分的独立袋子来实现,或者在第二次尝试拉另一个大理石之前,在它们被拉完后将它们替换掉。这些信息已经说明了独立性的性质,以及如何计算事件是否彼此独立。
现在,我们可以用这个信息来解决这个问题。问题要求我们确定购买卡车的概率是否与是否有手动变速箱无关。在这种情况下,我们需要调查下面的表达式是否正确:
首先,让我们计算一下在停车场找到一辆车的概率。
现在让我们计算一辆汽车有自动变速器的概率。
现在,我们需要计算这两个事件同时发生的概率。
现在,让我们看看下面的表达式是否正确:
利用这些信息,我们知道正确答案如下:
问题4:独立事件:Ccss.Math.Content.Hss Cp.A.2
汽车经销商负责汽车库存。他们决定注意停车场中汽车和卡车的数量,以及车辆的变速箱类型:自动还是手动。他们将这些数据输入到下面的表格中:
一个潜在的购车者想要购买一辆车,并询问车型是否独立于变速箱风格。根据数据,购买一辆独立于它的汽车是否拥有自动变速器?
为了解决与这个标准相关的问题,我们需要理解两个主要组成部分:概率和独立事件的性质。概率通常被定义为事件发生的机会或可能性。它是通过识别两个组件来计算的:事件和样本空间。事件被定义为我们希望看到的有利结果或成功。另一方面,样本空间被定义为事件所有可能结果的集合。在数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:掷骰子。我们想知道摇到1点的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
以分数形式表示的概率值将在0到1之间。1表示事件一定会发生,而0表示事件不会发生。同样,用百分比表示的概率值在0到100%之间,其中接近0的概率不太可能发生,接近100%的概率更有可能发生。
现在我们可以计算概率了,我们可以回顾一下独立事件的性质。独立事件的概率说明两个事件(A和B)是独立的,当且仅当事件A的概率乘以事件B的概率等于事件A和事件B的交集发生的概率。它可以写成如下表达式:
让我们回到骰子的例子。掷1对1骰子的概率和掷2骰子的概率是独立的吗?首先,让我们计算一下摇到1的概率。
现在,让我们求出在同一次骰子中另一个骰子掷到2的概率。
让我们把这两个概率相乘。
现在,让我们求出在两个不同的骰子上同时摇到1和2的概率。
让我们比较一下这两种可能性。
因此,概率是相等的,
让我们看另一个例子。一个人有一个装满10颗弹珠的袋子:6颗白色弹珠和4颗黑色弹珠。他想知道取出一颗白球的概率是否独立于取出一颗黑球的概率。让我们从计算取出一个黑色弹珠的概率开始。
现在让我们计算取出一个白色弹珠的概率。
让我们把这两个概率相乘。
现在让我们观察一下同时发生的这些事件。假设一个黑色的弹珠首先被从袋子里拿出来。黑色弹珠的概率如下:
这和以前一样;然而,取出白色弹珠的概率发生了变化,因为从袋子中取出了一颗弹珠。
两者发生的概率可以写成:
概率是不相等的。
这是因为这两个事件是相互依赖的。当一个弹珠在第一次抓取时被拉(无论它是黑的还是白的)并且没有被替换,在第二次抓取时被拉的弹珠总数是不同的。因此,从第一次事件到第二次事件,抽出特定颜色弹珠的概率发生了变化。这种情况可以通过使用两个具有相同大理石成分的独立袋子来实现,或者在第二次尝试拉另一个大理石之前,在它们被拉完后将它们替换掉。这些信息已经说明了独立性的性质,以及如何计算事件是否彼此独立。
现在,我们可以用这个信息来解决这个问题。问题要求我们确定购买卡车的概率是否与是否有手动变速箱无关。在这种情况下,我们需要调查下面的表达式是否正确:
首先,让我们计算一下在停车场找到一辆车的概率。
现在让我们计算一辆汽车有自动变速器的概率。
现在,我们需要计算这两个事件同时发生的概率。
现在,让我们看看下面的表达式是否正确:
利用这些信息,我们知道正确答案如下:
例5:独立事件:Ccss.Math.Content.Hss Cp.A.2
汽车经销商负责汽车库存。他们决定注意停车场中汽车和卡车的数量,以及车辆的变速箱类型:自动还是手动。他们将这些数据输入到下面的表格中:
一个潜在的购车者想要购买一辆车,并询问车型是否独立于变速箱风格。根据数据,购买一辆独立于它的汽车是否拥有自动变速器?
为了解决与这个标准相关的问题,我们需要理解两个主要组成部分:概率和独立事件的性质。概率通常被定义为事件发生的机会或可能性。它是通过识别两个组件来计算的:事件和样本空间。事件被定义为我们希望看到的有利结果或成功。另一方面,样本空间被定义为事件所有可能结果的集合。在数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:掷骰子。我们想知道摇到1点的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
以分数形式表示的概率值将在0到1之间。1表示事件一定会发生,而0表示事件不会发生。同样,用百分比表示的概率值在0到100%之间,其中接近0的概率不太可能发生,接近100%的概率更有可能发生。
现在我们可以计算概率了,我们可以回顾一下独立事件的性质。独立事件的概率说明两个事件(A和B)是独立的,当且仅当事件A的概率乘以事件B的概率等于事件A和事件B的交集发生的概率。它可以写成如下表达式:
让我们回到骰子的例子。掷1对1骰子的概率和掷2骰子的概率是独立的吗?首先,让我们计算一下摇到1的概率。
现在,让我们求出在同一次骰子中另一个骰子掷到2的概率。
让我们把这两个概率相乘。
现在,让我们求出在两个不同的骰子上同时摇到1和2的概率。
让我们比较一下这两种可能性。
因此,概率是相等的,
让我们看另一个例子。一个人有一个装满10颗弹珠的袋子:6颗白色弹珠和4颗黑色弹珠。他想知道取出一颗白球的概率是否独立于取出一颗黑球的概率。让我们从计算取出一个黑色弹珠的概率开始。
现在让我们计算取出一个白色弹珠的概率。
让我们把这两个概率相乘。
现在让我们观察一下同时发生的这些事件。假设一个黑色的弹珠首先被从袋子里拿出来。黑色弹珠的概率如下:
这和以前一样;然而,取出白色弹珠的概率发生了变化,因为从袋子中取出了一颗弹珠。
两者发生的概率可以写成:
概率是不相等的。
这是因为这两个事件是相互依赖的。当一个弹珠在第一次抓取时被拉(无论它是黑的还是白的)并且没有被替换,在第二次抓取时被拉的弹珠总数是不同的。因此,从第一次事件到第二次事件,抽出特定颜色弹珠的概率发生了变化。这种情况可以通过使用两个具有相同大理石成分的独立袋子来实现,或者在第二次尝试拉另一个大理石之前,在它们被拉完后将它们替换掉。这些信息已经说明了独立性的性质,以及如何计算事件是否彼此独立。
现在,我们可以用这个信息来解决这个问题。问题要求我们确定购买卡车的概率是否与是否有手动变速箱无关。在这种情况下,我们需要调查下面的表达式是否正确:
首先,让我们计算一下在停车场找到一辆车的概率。
现在让我们计算一辆汽车有自动变速器的概率。
现在,我们需要计算这两个事件同时发生的概率。
现在,让我们看看下面的表达式是否正确:
利用这些信息,我们知道正确答案如下:
例子问题6:独立事件:Ccss.Math.Content.Hss Cp.A.2
汽车经销商负责汽车库存。他们决定注意停车场中汽车和卡车的数量,以及车辆的变速箱类型:自动还是手动。他们将这些数据输入到下面的表格中:
一个潜在的购车者想要购买一辆车,并询问车型是否独立于变速箱风格。根据数据,购买一辆独立于它的汽车是否拥有自动变速器?
为了解决与这个标准相关的问题,我们需要理解两个主要组成部分:概率和独立事件的性质。概率通常被定义为事件发生的机会或可能性。它是通过识别两个组件来计算的:事件和样本空间。事件被定义为我们希望看到的有利结果或成功。另一方面,样本空间被定义为事件所有可能结果的集合。在数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:掷骰子。我们想知道摇到1点的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
以分数形式表示的概率值将在0到1之间。1表示事件一定会发生,而0表示事件不会发生。同样,用百分比表示的概率值在0到100%之间,其中接近0的概率不太可能发生,接近100%的概率更有可能发生。
现在我们可以计算概率了,我们可以回顾一下独立事件的性质。独立事件的概率说明两个事件(A和B)是独立的,当且仅当事件A的概率乘以事件B的概率等于事件A和事件B的交集发生的概率。它可以写成如下表达式:
让我们回到骰子的例子。掷1对1骰子的概率和掷2骰子的概率是独立的吗?首先,让我们计算一下摇到1的概率。
现在,让我们求出在同一次骰子中另一个骰子掷到2的概率。
让我们把这两个概率相乘。
现在,让我们求出在两个不同的骰子上同时摇到1和2的概率。
让我们比较一下这两种可能性。
因此,概率是相等的,
让我们看另一个例子。一个人有一个装满10颗弹珠的袋子:6颗白色弹珠和4颗黑色弹珠。他想知道取出一颗白球的概率是否独立于取出一颗黑球的概率。让我们从计算取出一个黑色弹珠的概率开始。
现在让我们计算取出一个白色弹珠的概率。
让我们把这两个概率相乘。
现在让我们观察一下同时发生的这些事件。假设一个黑色的弹珠首先被从袋子里拿出来。黑色弹珠的概率如下:
这和以前一样;然而,取出白色弹珠的概率发生了变化,因为从袋子中取出了一颗弹珠。
两者发生的概率可以写成:
概率是不相等的。
这是因为这两个事件是相互依赖的。当一个弹珠在第一次抓取时被拉(无论它是黑的还是白的)并且没有被替换,在第二次抓取时被拉的弹珠总数是不同的。因此,从第一次事件到第二次事件,抽出特定颜色弹珠的概率发生了变化。这种情况可以通过使用两个具有相同大理石成分的独立袋子来实现,或者在第二次尝试拉另一个大理石之前,在它们被拉完后将它们替换掉。这些信息已经说明了独立性的性质,以及如何计算事件是否彼此独立。
现在,我们可以用这个信息来解决这个问题。问题要求我们确定购买卡车的概率是否与是否有手动变速箱无关。在这种情况下,我们需要调查下面的表达式是否正确:
首先,让我们计算一下在停车场找到一辆车的概率。
现在让我们计算一辆汽车有自动变速器的概率。
现在,我们需要计算这两个事件同时发生的概率。
现在,让我们看看下面的表达式是否正确:
利用这些信息,我们知道正确答案如下:
示例问题7:独立事件:Ccss.Math.Content.Hss Cp.A.2
汽车经销商负责汽车库存。他们决定注意停车场中汽车和卡车的数量,以及车辆的变速箱类型:自动还是手动。他们将这些数据输入到下面的表格中:
一个潜在的购车者想要购买一辆车,并询问车型是否独立于变速箱风格。根据数据,购买一辆独立于它的汽车是否拥有自动变速器?
为了解决与这个标准相关的问题,我们需要理解两个主要组成部分:概率和独立事件的性质。概率通常被定义为事件发生的机会或可能性。它是通过识别两个组件来计算的:事件和样本空间。事件被定义为我们希望看到的有利结果或成功。另一方面,样本空间被定义为事件所有可能结果的集合。在数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:掷骰子。我们想知道摇到1点的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
以分数形式表示的概率值将在0到1之间。1表示事件一定会发生,而0表示事件不会发生。同样,用百分比表示的概率值在0到100%之间,其中接近0的概率不太可能发生,接近100%的概率更有可能发生。
现在我们可以计算概率了,我们可以回顾一下独立事件的性质。独立事件的概率说明两个事件(A和B)是独立的,当且仅当事件A的概率乘以事件B的概率等于事件A和事件B的交集发生的概率。它可以写成如下表达式:
让我们回到骰子的例子。掷1对1骰子的概率和掷2骰子的概率是独立的吗?首先,让我们计算一下摇到1的概率。
现在,让我们求出在同一次骰子中另一个骰子掷到2的概率。
让我们把这两个概率相乘。
现在,让我们求出在两个不同的骰子上同时摇到1和2的概率。
让我们比较一下这两种可能性。
因此,概率是相等的,
让我们看另一个例子。一个人有一个装满10颗弹珠的袋子:6颗白色弹珠和4颗黑色弹珠。他想知道取出一颗白球的概率是否独立于取出一颗黑球的概率。让我们从计算取出一个黑色弹珠的概率开始。
现在让我们计算取出一个白色弹珠的概率。
让我们把这两个概率相乘。
现在让我们观察一下同时发生的这些事件。假设一个黑色的弹珠首先被从袋子里拿出来。黑色弹珠的概率如下:
这和以前一样;然而,取出白色弹珠的概率发生了变化,因为从袋子中取出了一颗弹珠。
两者发生的概率可以写成:
概率是不相等的。
这是因为这两个事件是相互依赖的。当一个弹珠在第一次抓取时被拉(无论它是黑的还是白的)并且没有被替换,在第二次抓取时被拉的弹珠总数是不同的。因此,从第一次事件到第二次事件,抽出特定颜色弹珠的概率发生了变化。这种情况可以通过使用两个具有相同大理石成分的独立袋子来实现,或者在第二次尝试拉另一个大理石之前,在它们被拉完后将它们替换掉。这些信息已经说明了独立性的性质,以及如何计算事件是否彼此独立。
现在,我们可以用这个信息来解决这个问题。问题要求我们确定购买卡车的概率是否与是否有手动变速箱无关。在这种情况下,我们需要调查下面的表达式是否正确:
首先,让我们计算一下在停车场找到一辆车的概率。
现在让我们计算一辆汽车有自动变速器的概率。
现在,我们需要计算这两个事件同时发生的概率。
现在,让我们看看下面的表达式是否正确:
利用这些信息,我们知道正确答案如下:
例8:独立事件:Ccss.Math.Content.Hss Cp.A.2
汽车经销商负责汽车库存。他们决定注意停车场中汽车和卡车的数量,以及车辆的变速箱类型:自动还是手动。他们将这些数据输入到下面的表格中:
一个潜在的购车者想要购买一辆车,并询问车型是否独立于变速箱风格。根据数据,购买一辆独立于它的汽车是否拥有自动变速器?
为了解决与这个标准相关的问题,我们需要理解两个主要组成部分:概率和独立事件的性质。概率通常被定义为事件发生的机会或可能性。它是通过识别两个组件来计算的:事件和样本空间。事件被定义为我们希望看到的有利结果或成功。另一方面,样本空间被定义为事件所有可能结果的集合。在数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:掷骰子。我们想知道摇到1点的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
以分数形式表示的概率值将在0到1之间。1表示事件一定会发生,而0表示事件不会发生。同样,用百分比表示的概率值在0到100%之间,其中接近0的概率不太可能发生,接近100%的概率更有可能发生。
现在我们可以计算概率了,我们可以回顾一下独立事件的性质。独立事件的概率说明两个事件(A和B)是独立的,当且仅当事件A的概率乘以事件B的概率等于事件A和事件B的交集发生的概率。它可以写成如下表达式:
让我们回到骰子的例子。掷1对1骰子的概率和掷2骰子的概率是独立的吗?首先,让我们计算一下摇到1的概率。
现在,让我们求出在同一次骰子中另一个骰子掷到2的概率。
让我们把这两个概率相乘。
现在,让我们求出在两个不同的骰子上同时摇到1和2的概率。
让我们比较一下这两种可能性。
因此,概率是相等的,
让我们看另一个例子。一个人有一个装满10颗弹珠的袋子:6颗白色弹珠和4颗黑色弹珠。他想知道取出一颗白球的概率是否独立于取出一颗黑球的概率。让我们从计算取出一个黑色弹珠的概率开始。
现在让我们计算取出一个白色弹珠的概率。
让我们把这两个概率相乘。
现在让我们观察一下同时发生的这些事件。假设一个黑色的弹珠首先被从袋子里拿出来。黑色弹珠的概率如下:
这和以前一样;然而,取出白色弹珠的概率发生了变化,因为从袋子中取出了一颗弹珠。
两者发生的概率可以写成:
概率是不相等的。
这是因为这两个事件是相互依赖的。当一个弹珠在第一次抓取时被拉(无论它是黑的还是白的)并且没有被替换,在第二次抓取时被拉的弹珠总数是不同的。因此,从第一次事件到第二次事件,抽出特定颜色弹珠的概率发生了变化。这种情况可以通过使用两个具有相同大理石成分的独立袋子来实现,或者在第二次尝试拉另一个大理石之前,在它们被拉完后将它们替换掉。这些信息已经说明了独立性的性质,以及如何计算事件是否彼此独立。
现在,我们可以用这个信息来解决这个问题。问题要求我们确定购买卡车的概率是否与是否有手动变速箱无关。在这种情况下,我们需要调查下面的表达式是否正确:
首先,让我们计算一下在停车场找到一辆车的概率。
现在让我们计算一辆汽车有自动变速器的概率。
现在,我们需要计算这两个事件同时发生的概率。
现在,让我们看看下面的表达式是否正确:
利用这些信息,我们知道正确答案如下:
问题9:独立事件:Ccss.Math.Content.Hss Cp.A.2
汽车经销商负责汽车库存。他们决定注意停车场中汽车和卡车的数量,以及车辆的变速箱类型:自动还是手动。他们将这些数据输入到下面的表格中:
一个潜在的购车者想要购买一辆车,并询问车型是否独立于变速箱风格。根据数据,购买一辆独立于它的汽车是否拥有自动变速器?
为了解决与这个标准相关的问题,我们需要理解两个主要组成部分:概率和独立事件的性质。概率通常被定义为事件发生的机会或可能性。它是通过识别两个组件来计算的:事件和样本空间。事件被定义为我们希望看到的有利结果或成功。另一方面,样本空间被定义为事件所有可能结果的集合。在数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:掷骰子。我们想知道摇到1点的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
以分数形式表示的概率值将在0到1之间。1表示事件一定会发生,而0表示事件不会发生。同样,用百分比表示的概率值在0到100%之间,其中接近0的概率不太可能发生,接近100%的概率更有可能发生。
现在我们可以计算概率了,我们可以回顾一下独立事件的性质。独立事件的概率说明两个事件(A和B)是独立的,当且仅当事件A的概率乘以事件B的概率等于事件A和事件B的交集发生的概率。它可以写成如下表达式:
让我们回到骰子的例子。掷1对1骰子的概率和掷2骰子的概率是独立的吗?首先,让我们计算一下摇到1的概率。
现在,让我们求出在同一次骰子中另一个骰子掷到2的概率。
让我们把这两个概率相乘。
现在,让我们求出在两个不同的骰子上同时摇到1和2的概率。
让我们比较一下这两种可能性。
因此,概率是相等的,
让我们看另一个例子。一个人有一个装满10颗弹珠的袋子:6颗白色弹珠和4颗黑色弹珠。他想知道取出一颗白球的概率是否独立于取出一颗黑球的概率。让我们从计算取出一个黑色弹珠的概率开始。
现在让我们计算取出一个白色弹珠的概率。
让我们把这两个概率相乘。
现在让我们观察一下同时发生的这些事件。假设一个黑色的弹珠首先被从袋子里拿出来。黑色弹珠的概率如下:
这和以前一样;然而,取出白色弹珠的概率发生了变化,因为从袋子中取出了一颗弹珠。
两者发生的概率可以写成:
概率是不相等的。
这是因为这两个事件是相互依赖的。当一个弹珠在第一次抓取时被拉(无论它是黑的还是白的)并且没有被替换,在第二次抓取时被拉的弹珠总数是不同的。因此,从第一次事件到第二次事件,抽出特定颜色弹珠的概率发生了变化。这种情况可以通过使用两个具有相同大理石成分的独立袋子来实现,或者在第二次尝试拉另一个大理石之前,在它们被拉完后将它们替换掉。这些信息已经说明了独立性的性质,以及如何计算事件是否彼此独立。
现在,我们可以用这个信息来解决这个问题。问题要求我们确定购买卡车的概率是否与是否有手动变速箱无关。在这种情况下,我们需要调查下面的表达式是否正确:
首先,让我们计算一下在停车场找到一辆车的概率。
现在让我们计算一辆汽车有自动变速器的概率。
现在,我们需要计算这两个事件同时发生的概率。
现在,让我们看看下面的表达式是否正确:
利用这些信息,我们知道正确答案如下:
例子问题10:独立事件:Ccss.Math.Content.Hss Cp.A.2
汽车经销商负责汽车库存。他们决定注意停车场中汽车和卡车的数量,以及车辆的变速箱类型:自动还是手动。他们将这些数据输入到下面的表格中:
一个潜在的购车者想要购买一辆车,并询问车型是否独立于变速箱风格。根据数据,购买一辆独立于它的汽车是否拥有自动变速器?
为了解决与这个标准相关的问题,我们需要理解两个主要组成部分:概率和独立事件的性质。概率通常被定义为事件发生的机会或可能性。它是通过识别两个组件来计算的:事件和样本空间。事件被定义为我们希望看到的有利结果或成功。另一方面,样本空间被定义为事件所有可能结果的集合。在数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:掷骰子。我们想知道摇到1点的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
以分数形式表示的概率值将在0到1之间。1表示事件一定会发生,而0表示事件不会发生。同样,用百分比表示的概率值在0到100%之间,其中接近0的概率不太可能发生,接近100%的概率更有可能发生。
现在我们可以计算概率了,我们可以回顾一下独立事件的性质。独立事件的概率说明两个事件(A和B)是独立的,当且仅当事件A的概率乘以事件B的概率等于事件A和事件B的交集发生的概率。它可以写成如下表达式:
让我们回到骰子的例子。掷1对1骰子的概率和掷2骰子的概率是独立的吗?首先,让我们计算一下摇到1的概率。
现在,让我们求出在同一次骰子中另一个骰子掷到2的概率。
让我们把这两个概率相乘。
现在,让我们求出在两个不同的骰子上同时摇到1和2的概率。
让我们比较一下这两种可能性。
因此,概率是相等的,
让我们看另一个例子。一个人有一个装满10颗弹珠的袋子:6颗白色弹珠和4颗黑色弹珠。他想知道取出一颗白球的概率是否独立于取出一颗黑球的概率。让我们从计算取出一个黑色弹珠的概率开始。
现在让我们计算取出一个白色弹珠的概率。
让我们把这两个概率相乘。
现在让我们观察一下同时发生的这些事件。假设一个黑色的弹珠首先被从袋子里拿出来。黑色弹珠的概率如下:
这和以前一样;然而,取出白色弹珠的概率发生了变化,因为从袋子中取出了一颗弹珠。
两者发生的概率可以写成:
概率是不相等的。
这是因为这两个事件是相互依赖的。当一个弹珠在第一次抓取时被拉(无论它是黑的还是白的)并且没有被替换,在第二次抓取时被拉的弹珠总数是不同的。因此,从第一次事件到第二次事件,抽出特定颜色弹珠的概率发生了变化。这种情况可以通过使用两个具有相同大理石成分的独立袋子来实现,或者在第二次尝试拉另一个大理石之前,在它们被拉完后将它们替换掉。这些信息已经说明了独立性的性质,以及如何计算事件是否彼此独立。
现在,我们可以用这个信息来解决这个问题。问题要求我们确定购买卡车的概率是否与是否有手动变速箱无关。在这种情况下,我们需要调查下面的表达式是否正确:
首先,让我们计算一下在停车场找到一辆车的概率。
现在让我们计算一辆汽车有自动变速器的概率。
现在,我们需要计算这两个事件同时发生的概率。
现在,让我们看看下面的表达式是否正确:
利用这些信息,我们知道正确答案如下: