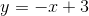Call Now to Set Up Tutoring:

(888) 888-0446

一个P Calculus AB : Tangent line to a curve at a point and local linear approximation

年代tudy concepts, example questions & explanations for AP Calculus AB

Create An Account Create Tests & Flashcards

一个ll AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 Next →

Example Question #1 :Derivatives

Differentiate,

$y = \sin(\sin(\sin\(3x)))$

Possible Answers:

$\frac{dy}{dx}=3\cos(\sin(\sin(x)))\times \sin(\sin(x))\times \cos(3x)$

$\frac{dy}{dx}=3\cos(\cos(\sin(3x)))\times \sin(\sin(3x))\times \sin(3x)$

$\frac{dy}{dx}=3\cos(\sin(\sin(3x)))\times \cos(\sin(3x))\times \cos(3x)$

$\frac{dy}{dx}=3\cos(\cos(\sin(3x)))\times \cos(\sin(3x))$

$\frac{dy}{dx}=3\cos(\sin(\sin(3x)))\times \cos(\sin(3x))$

Correct answer:

$\frac{dy}{dx}=3\cos(\sin(\sin(3x)))\times \cos(\sin(3x))\times \cos(3x)$

Explanation:

Differentiate,

$y = \sin(\sin(\sin\(3x)))$

年代trategy

This one at first glance appears difficult even if we recognize that the chain rule is needed; we have a function within a function within a function within a function. To avoid making mistakes, it's best to start by defining variables to make the calculation easier to follow.

Let's start with the outermost function, we will writeas a function ofby setting,

$u = \sin(\sin(3x))$

______________________________________________________

$y = \sin(\underset{u}{ \underbrace{\sin(\sin(3x))}}) = \sin(u)$

$y = \sin(u)$

_______________________________________________________

年代imilarly, defineto writeas a function of

$u = \sin(\underset{v}{ \underbrace{\sin(3x)}}) = \sin(v)$

$u = \sin(v)$

_______________________________________________________

Writeas a function of

$v = \sin(\underset{w}{ \underbrace{3x}} )=\sin(w)$

$v = \sin(w)$

_______________________________________________________

Finally, define the inner-most function,, as the function of

w=3x

________________________________________________________

$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dv}\frac{dv}{dw}\frac{dw}{dx}$

年代ince $\frac{dw}{dx}=3$ we will just substitute that in and move to the front.

$\frac{dy}{dx}=3\cos(u)\cos(v)\cos(w)$

That was easy enough, now just write everything in terms ofby going back to the definitions of和.

$u = \sin(\sin(3x))$

$v = \sin(3x)$

w = 3x

$\frac{dy}{dx}=3\cos(\sin(\sin(3x)))\times \cos(\sin(3x))\times \cos(3x)$

Report an Error

Example Question #1 :一个p Calculus Ab

Find the tangent line. Given the point (1,2)

y= x^2-3x+4

Possible Answers:

y=-x+3

y=x-2

y= x+2

y=x-6

y=x-4

Correct answer:

y=-x+3

Explanation:

To find the tangent line at the given point, we need to first take the derivative of the given function.

Power Rule:

Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent.

Therefore, y= x^2-3x+4 becomes y' = 2x - 3

From there we plug in the "1" from the point to get our m value of the equation y=mx + b . When we plug in "1" to y' we get m=-1. Then from there, we will plug our point intonow that we have found m to find our b value. So,

2=(-1)(1) + b

b= 3

Therefore, the tangent line is equal to

y= -x+3

Report an Error

Example Question #3 :Derivatives

Find the line tangent at the point (0,1)

$y=e^{3x}$

Possible Answers:

y=3x+2

y=3x-2

y=3x+3

y=-3x+2

y=3x+1

Correct answer:

y=3x+1

Explanation:

To find the tangent line at the given point, we need to first take the derivative of the given function. The rule for functions with "e" in it says that the derivative of e^x=e^x However with this function there is also a 3 in the exponent so we will also use chain rule. Chain Rules states that we work from the outside to the inside. Meaning we will take the derivative of the outside of the equation and multiply it by the derivative of the inside of the equation.

To put this into equation it will look like $3e^{3x}$

From there we plug in the "0" from the point to get our m value of the equation . When we plug in "0" to y' we get m=3. Then from there, we will plug our point into y=mx + b now that we have found m to find our m value. So,

1=3(0)+b

b=1 then plug this all back into the equation once more and we are left with

y=3x + 1

Report an Error

Example Question #4 :Derivatives

Find the tangent line given the point (2,4) and the equation

y=2x^2 + 4x

Possible Answers:

y=8x-12

y=-8x-12

y=28x-16

y=-8x+12

y=8x+12

Correct answer:

y=8x-12

Explanation:

To find the tangent line at the given point, we need to first take the derivative of the given function using Power Rule

Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent. $(nx^{^{n-1}})$

From there we plug in the "2" from the point to get our m value of the equation . When we plug in "2" to y' we get m=8. Then from there, we will plug our point into now that we have found m to find our b value. So,

y=mx+b

4=8(2) + b ; b=-12

Plug this back into y=mx+b

y= 8x - 12

Report an Error

Example Question #5 :Derivatives

Find the equation of the line tangent to the curve at the point where $x = \frac{\pi}{4}$

$f(x)=\tan(x)+x$

Possible Answers:

$y = \sqrt{3}x+\pi$

$y = 3x - \frac{3\pi}{4}$

$y = 3x+\frac{2-\pi}{2}$

$y = x+\frac{4-\pi}{2}$

$y = \sqrt{2}x+\frac{\pi}{4}$

Correct answer:

$y = 3x+\frac{2-\pi}{2}$

Explanation:

Find the equation of the line tangent to the curveat the given point

$f(x)=\tan(x)+x$ $x = \frac{\pi}{4}$

The slope of the line tangent at the given point will be equal to the derivative of f(x) at that point. Compute the derivative and find the slope for our line:

$f'(x)=\sec^2(x)+1$

$f'\left(\frac{\pi}{4} \right )=\sec^2\left(\frac{\pi}{4}\right)+1$

Evaluate the secant term:

$\sec^2\left(\frac{\pi}{4}\right)=\frac{1}{\cos^2\left(\frac{\pi}{4}\right)}=\left(\frac{2}{\sqrt{2}} \right )^2=2$

Therefore slope of the tangent line is simply:

$f'\left(\frac{\pi}{4} \right )=3$

年代o now we know the slope of the tangent line and can write the equation then solve for

y = 3x+b

In order to solve forwe need one point on the line. Use the point where the tangent line meets the curve. Use the original function to find the "y" coordinate at this point:

$f\left(\frac{\pi}{4} \right )\: \: =\: \: \tan\left(\frac{\pi}{4}\right) +\frac{\pi}{4}\: \:=\: \: 1+\frac{\pi}{4}\: \: =\: \: \frac{4+\pi}{4}$

We now have our point:

$\left(\frac{\pi}{4}\: \: ,\: \frac{4+\pi}{4}\right )$

Use the point to find

$\frac{4+\pi}{4}=3\left(\frac{\pi}{4} \right )+b$

$b = \frac{2-\pi}{2}$

$y = 3x+\frac{2-\pi}{2}$

Report an Error

Example Question #6 :Derivatives

Find the slope of the line tangent to the curve of d(g) when g=6.

d(g)=14g^3+6g^2-2g+12

Possible Answers:

d'(g)=84g+12

d'(6)=1486

d'(6)=1582

d'(g)=42g^2+12g-2g+12

Correct answer:

d'(6)=1582

Explanation:

Find the slope of the line tangent to the curve of d(g) when g=6.

d(g)=14g^3+6g^2-2g+12

一个ll we need here is the power rule. This states that to find the derivative of a polynomial, simply subtract 1 from each exponent and then multiply each term by their original exponent.

Constant terms will drop out when we do this, and linear terms will become constants.

d(g)=14g^3+6g^2-2g+12

d'(g)=(3)14g^2+(2)6g-2=42g^2+12g-2

d'(g)=42g^2+12g-2

From here substitute in g=6.

$\\d'(6)=42(6)^2+12(6)-2 \\d'(6)=1582$

Report an Error

Example Question #7 :Derivatives

Give the equation of the line tangent to the graph of the equation

$f(x) = 4x+ e^{x-2}$

at the point (2, 9) .

Possible Answers:

y = 5x-1

y=6x-3

y= (4+e)x+(1-2e)

y=4x+1

y= (4-e)x+(1+2e)

Correct answer:

y = 5x-1

Explanation:

The tangent line to the graph ofat point (2, 9) is the line with slope f'(2) that passes through that point. Find the derivative f'(x) :

$f(x) = 4x+ e^{x-2}$

$f(x) = 4x+ \frac{1}{e^{2}} \cdot e^{x}$

$f'(x) =\frac{\mathrm{d} }{\mathrm{d} x} \left (4x+ \frac{1}{e^{2}} \cdot e^{x} \right )$

一个pply the sum rule:

$f'(x) =\frac{\mathrm{d} }{\mathrm{d} x} (4x ) + \frac{\mathrm{d} }{\mathrm{d} x} \left ( \frac{1}{e^{2}} \cdot e^{x} \right )$

$f'(x) =\frac{\mathrm{d} }{\mathrm{d} x} (4x ) + \frac{1}{e^{2}} \frac{\mathrm{d} }{\mathrm{d} x} \left ( e^{x} \right )$

$f'(x) =4 + \frac{1}{e^{2}} e^{x}$

$f'(x) =4 + e^{x-2}$

$f'(2)= 4 + e^{2-2} = 4 + e^{0} = 4 + 1 = 5$

The tangent line is therefore the line with slope 5 through (2, 9) .Apply the point-slope formula:

y - 9 = 5(x-2)

y - 9 =5x-10

y = 5x-1

Report an Error

Example Question #8 :Derivatives

Give the equation of the line tangent to the graph of the equation

$f(x) =3 \sin \frac{x}{2} +2 \cos \frac{x}{3}$

at the point (0, 2) .

Possible Answers:

$y = \frac{5}{6}x+2$

None of the other choices gives the correct response.

$y = \frac{2}{3}x+2$

$y = -\frac{5}{6}x+2$

$y =- \frac{2}{3}x+2$

Correct answer:

None of the other choices gives the correct response.

Explanation:

The tangent line to the graph ofat point (0, 2) is the line with slope f'(0) that passes through that point. Find the derivative f'(x) :

$f(x) =3 \sin \frac{x}{2} +2 \cos \frac{x}{3}$

$f'(x) =\frac{\mathrm{d} }{\mathrm{d} x}\left (3 \sin \frac{x}{2} +2 \cos \frac{x}{3} \right )$

一个pply the constant multiple and sum rules:

$f'(x) =\frac{\mathrm{d} }{\mathrm{d} x}\left (3 \sin \frac{x}{2} +2 \cos \frac{x}{3} \right )$

$f'(x) =\frac{\mathrm{d} }{\mathrm{d} x}\left (3 \sin \frac{x}{2} \right )+ \frac{\mathrm{d} }{\mathrm{d} x}\left ( 2 \cos \frac{x}{3} \right )$

$f'(x) =3 \frac{\mathrm{d} }{\mathrm{d} x}\left ( \sin \frac{x}{2} \right )+2 \frac{\mathrm{d} }{\mathrm{d} x}\left ( \cos \frac{x}{3} \right )$

年代et $u = \frac{x}{2}$ 和 $v= \frac{x}{3}$ 和apply the chain rule.

$f'(x) =3 \frac{\mathrm{d} }{\mathrm{d} x}\left ( \sin u \right )+2 \frac{\mathrm{d} }{\mathrm{d} x}\left ( \cos v \right )$

$f'(x) =3 \frac{\mathrm{d} u}{\mathrm{d} x}\cdot \frac{\mathrm{d} }{\mathrm{d} u} \left ( \sin u \right )+2 \frac{\mathrm{d} v}{\mathrm{d} x}\cdot \frac{\mathrm{d} }{\mathrm{d} v} \left ( \cos v \right )$

$f'(x) =3 \frac{\mathrm{d} u}{\mathrm{d} x}\cdot \cos u +2 \frac{\mathrm{d} v}{\mathrm{d} x}\cdot (- \sin v)$

年代ubstituting back:

$f'(x) =3 \frac{\mathrm{d} }{\mathrm{d} x} \left ( \frac{x}{2} \right )\cdot \cos \frac{x}{2} -2 \frac{\mathrm{d} }{\mathrm{d} x}\left ( \frac{x}{3} \right )\cdot \sin \frac{x}{3}$

$f'(x) =3 \left ( \frac{1}{2} \right )\cdot \cos \frac{x}{2} -2 \left ( \frac{1}{3} \right )\cdot \sin \frac{x}{3}$

$f'(x) = \frac{3}{2} \cos \frac{x}{2} - \frac{2}{3} \sin \frac{x}{3}$

Evaluate f'(0) using substitution:

$f'(0) = \frac{3}{2} \cos \frac{0}{2} - \frac{2}{3} \sin \frac{0}{3}$

$f'(0) = \frac{3}{2} \cos 0 - \frac{2}{3} \sin 0$

$f'(0) = \frac{3}{2}(1) - \frac{2}{3}( 0)$

$f'(0) = \frac{3}{2}$

The tangent line is therefore the line with slope $\frac{3}{2}$ through (0, 2) . (0, 2) is a-intercept, so apply the slope-intercept formula to get the equation

$y = \frac{3}{2}x+2$ .

This is not among the choices given.

Report an Error

Example Question #9 :Derivatives

Find the equation of the line parallel to the function y=4x^3+2 at x=1 , and passes through the point (2,4)

Possible Answers:

y=12x-20

y=15x-2

y=5x-10

y=-6x+3

Correct answer:

y=12x-20

Explanation:

We first start by finding the slope of the line in question, which we do by taking the derivative of y=4x^3+2 和evaluate at x=1 .

y'=12x^2 , y'(1)=12=m

We then use point slope form to get the equation of the line at the point (2,4)

(y-4)=12(x-2)

y=12x-20

Report an Error

Example Question #10 :Derivatives

Find the equation of the line tangent to $f(x)=x^{3}-3x^{2}+2x+4$ at the point (1,4) .

Possible Answers:

y=-2x+5

y=-x+5

y=-5x+1

y=x+1

$y=3x^{2}+2x+4$

Correct answer:

y=-x+5

Explanation:

The first step is to find the derivative of the function given, which is $f'(x)=3x^{2}-6x+2$ . Next, find the slope at (1,4) by plugging in x=1 and solving for f'(x) , which is the slope. You should get f'(1)= -1 . This means the slope of the new line is also -1 because at the point where a slope and a line are tangent they have the same slope. Use the equation y=mx+b to express your line. Y and x are variables and m is the slope, so the only thing you need to find is b. Plug in the point and slope into y=mx+b to get b=5 . Now you can express the general equation of the line as y=-x+5 .

Report an Error

← Previous 1 2 Next →

View AP Calculus AB Tutors

Chandana
Certified Tutor

University of Colombo, Bachelor of Science, Mathematics. University of Wyoming, Doctor of Philosophy, Mathematics.

View AP Calculus AB Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View AP Calculus AB Tutors

一个bhisek
Certified Tutor

佛罗里达大学工程学士,有限公司mputer Science.

一个ll AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

年代一个T Tutors in Boston,GMAT Tutors in Philadelphia,LSAT Tutors in San Diego,年代panish Tutors in Los Angeles,Reading Tutors in Los Angeles,GMAT Tutors in Miami,LSAT Tutors in Atlanta,Math Tutors in New York City,年代tatistics Tutors in Washington DC,一个lgebra Tutors in Houston

Popular Courses & Classes

MCAT Courses & Classes in Dallas Fort Worth,在洛杉矶GMAT考试课程和课程,GRE Courses & Classes in Boston,一个CT Courses & Classes in San Diego,MCAT Courses & Classes in Chicago,年代年代一个T Courses & Classes in Los Angeles,ISEE Courses & Classes in Miami,GRE Courses & Classes in Houston,GRE Courses & Classes in Chicago,MCAT Courses & Classes in San Diego

Popular Test Prep

ISEE Test Prep in Seattle,LSAT Test Prep in Seattle,LSAT Test Prep in Philadelphia,MCAT Test Prep in Miami,GMAT Test Prep in Los Angeles,GMAT Test Prep in Dallas Fort Worth,年代一个T Test Prep in San Diego,年代一个T Test Prep in Philadelphia,一个CT Test Prep in Houston,MCAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

一个physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

年代end your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
年代t. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

*Full legal name

Company name

*Phone number

*Email address

一个ddress

*一个ddress1

一个ddress2

*City

*年代tate

*Zipcode

*Country

Complaint Details

*URL of copyrighted work (where your original material is located)

*Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

*年代ignature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

年代earch 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

年代earch 350+ Subjects

一个P Calculus AB : Tangent line to a curve at a point and local linear approximation

年代tudy concepts, example questions & explanations for AP Calculus AB

一个ll AP Calculus AB Resources

Example Questions

Example Question #1 :Derivatives

Example Question #1 :一个p Calculus Ab

Example Question #3 :Derivatives

Example Question #4 :Derivatives

Example Question #5 :Derivatives

Example Question #6 :Derivatives

Example Question #7 :Derivatives

Example Question #8 :Derivatives

Example Question #9 :Derivatives

Example Question #10 :Derivatives

一个ll AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

一个ddress

Complaint Details

Find the Best Tutors

Email address:
Your name:
Feedback: