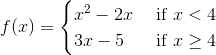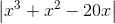1）如果一个函数是可微的，那么根据可微性的定义极限由，

的存在。因此(1)是必需的根据可微性的定义。_______________________________________________________________

2）如果一个函数在某一点上是可微的那么它在这一点上也是连续的。(反之亦然)。

函数在一点上是连续的我们必须有:

因此(2)和(4)是必需的。

-----------------------------------------------------------------------------------------

3）

这不是必须的，方程左边是一点处导数的定义为一个函数．一点处的导数不一定等于函数值在这一点，它等于坡在这一点上。因此3不一定是真的。

然而，我们可以注意到，对于一个给定的点，函数和它的导数是有可能相等的。例如，正弦和余弦会周期性相交。另一个例子是指数函数它的'导数'是什么．

______________________________________________________________

4)看到2

_______________________________________________________________

5)

同样，函数不一定要接近它的导数的极限。一个函数有可能以这种方式表现，例如正弦函数和它的导数余弦函数，它们在交点处有相同的极限。

根据可微性的定义，当极限存在时。当存在，我们说函数在点是可微的”。

所有的函数都是可微的．如果你观察每一个函数的图，它们都定义在不要有弯角、尖角或跳跃;它们都是平滑的，连接的(不一定是到处，只是在)．此外，不可能有一个函数在某一点上是可微的，但在同一点上不是连续的;differentiablity意味着连续性。

要回答这个问题，我们必须找到一个满足两个条件的方程:

(1)它的两侧必须有限制它们接近相同的值而且(2)它一定有一个洞．

每个可能的答案都提供了证明(1)和(2)的每种组合的情况。也就是说，一些方程包括这两个极限和y值，都没有,或者，在分段函数的情况下，一个不存在的y值和一个极限。

的函数,，分子因子为

而分母的因子是．因此，这张图

函数类似于，但有一个洞．因此,限制

在存在，即使y值在．