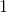Explanation:

To find the first derivative, we can use the power rule. To do that, we lower the exponent on the variables by one and multiply by the original exponent.

We're going to treatassince anything to the zero power is one.

Notice thatsince anything times zero is zero.

Explanation:

We use the power rule on each term of the function.

The first term

becomes

.

The second term

becomes

.

The final term, 7, is a constant, so its derivative is simply zero.

Explanation:

We are not going to evaluate this directly. Looking at the function, it seems very similar to the definition of a derivative of some kind of trigonometric function. We will look at the definition of a derivative to find a function that would have a derivative defined by this limit.

In otherwords, we wish to identify a functionsuch that its' derivativeis the function.

Let's findsuch that:

有限公司mpare corresponding terms in the numerators in the above expressions.

By inspection, these terms clearly indicate that our functionmust be of the form:

_______________________________________________________________

Side note

If your confused by the inclusion of the arbitrary constant, note that when we differentiate this function the constant term will vanish since the derivative of a constant is zero. You can also see that in applying the definition of a derivative, if I included the constant in the two terms in the numerator,

the constant "C" would vanish when we subtract the latter from the former,.

Therefore, even if you didn't consider the constantwhen working out the function, it would not have changed the result

_______________________________________________________________

Because we know that

,

Simply differentiateto find,

Therefore,

Or to put it another way,

Explanation:

This limit can't be evaluated by conventional limit laws. To see why the answer is, we have to recognize that the limit looks like

, with.

This new limit is a conventional expression for, withsubstituted in for

We can findwith the power rule, and substitutinggives.

To summarize, since

, we have

.

Explanation:

There are two commonly used formulations of the difference quotient used to compute derviatives. Both definitions are equivalent and should always give the same derivative for a given function.

The limit in this particular problem resembles the first difference quotient listed above.

By inspection, it's clear that thein our case must be. We are being asked to evaluate the limit by interpreting it as the definition of the derivative of a function. We must therefore identify the function, which is clearly, and then differentiate it using known rules of differentiation.

First rewrite the function to apply the rule for:

This means

Explanation:

The difference quotient of a functionis the expression

.

If, this expression is

Explanation:

The derivative of a functioncan be defined according to the following:

Using this for our function - and not forgetting to write the limit for every step! - we get

Explanation:

The derivative of a function as defined by the limit of the difference quotient is

Evaluating the limit using our function - and always writing the limit symbol! - we get

Explanation:

To find the derivative using the limit of the difference quotient, we use the formula:

Explanation: