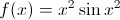我们周六和周日开放!

现在打电话设置辅导:

(888) 888 - 0446

AP微积分AB:点上的导数

学习AP微积分AB的概念，示例问题和解释

创建帐户创建测试和抽认卡

所有AP微积分AB资源

3诊断测试 164练习题今日问题抽认卡概念学习

例子问题

←之前 1 2 3. 4 5 6 7 8 9 10 11 12 下一个→

问题62:A点导数

求经过(- 1,1)并垂直于x=4处与以下函数相切的直线的方程:

f(x)=x^3

可能的答案:

y=-{48}x+49

y={48}x+49

$y=-\frac{x}{48}+\frac{47}{48}$

$y=\frac{x}{48}+\frac{47}{48}$

正确答案:

$y=-\frac{x}{48}+\frac{47}{48}$

解释：

为了确定直线的方程，我们必须首先求出它的斜率，这个斜率垂直于函数的切线的斜率。函数在任意点的切线由函数的一阶导数给出:

f'(x)=3x^2

导数是用下面的规则求出来的:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

求在给定点的导数，我们发现函数的切线斜率为

f'(4)=48

然而，它的负倒数——切线的斜率——是

$-\frac{1}{48}$

现在我们可以用点斜式来表示直线的方程

$y-1=-\frac{1}{48}(x+1)$

$y=-\frac{x}{48}+\frac{47}{48}$

报告错误

问题63:A点导数

求出经过(4,10)并与以下函数在x=2处的切线平行的直线方程:

$f=\ln(x^2-x)$

可能的答案:

$y=-\frac{2}{3}x+16$

y=x

$y=\frac{3}{2}x+4$

$y=\frac{3}{2}x$

正确答案:

$y=\frac{3}{2}x+4$

解释：

为了确定直线的方程，我们必须首先求出它的斜率，它平行于函数的切线的斜率。函数在任意点的切线由函数的一阶导数给出:

$f'=\frac{2x-1}{x^2-x}$

这是使用以下规则发现的:

$\frac{\mathrm{d} }{\mathrm{d} x} \ln(u)=\frac{1}{u}\cdot \frac{\mathrm{d} u}{\mathrm{d} x}$ ， $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ ， $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

现在，我们通过将该点代入一阶导数函数求出该点处的切线斜率

$f'(2)=\frac{3}{2}$

现在，我们用点斜式来求直线方程

$y-10=\frac{3}{2}(x-4)$

$y=\frac{3}{2}x+4$

报告错误

问题64:A点导数

求出经过(3,1)并与以下函数在x=2处的切线平行的直线的方程:

f=x^3-1

可能的答案:

y=12x-35

y=12x-2

没有其他答案

y=x

y=27

正确答案:

y=12x-35

解释：

为了确定直线的方程，我们必须首先求出它的斜率，它平行于函数的切线的斜率。函数在任意点的切线由函数的一阶导数给出:

f'=3x^2

下面的规则用于求导数:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

求在给定点的导数，我们发现函数的切线斜率为

3(2^2)=12=m

现在我们可以用点斜式来表示直线的方程

y-1=12(x-3)

y=12x-35

报告错误

示例问题161:衍生品

求出经过(2,0)且垂直于以下函数在x=0处的切线的方程:

$f=\ln(2-x)$

可能的答案:

y=2x-4

y=-2x+4

$y=-\frac{1}{2}x+1$

$y=-\frac{1}{2}x+3$

正确答案:

y=2x-4

解释：

要确定直线的方程，我们必须先求出它的斜率，也就是垂直的与函数的切线之比。函数在任意点的切线由函数的一阶导数给出:

$f'=\frac{-1}{2-x}$

这是使用以下规则发现的:

$\frac{\mathrm{d} }{\mathrm{d} x} \ln(u)=\frac{1}{u}\frac{\mathrm{d} u}{\mathrm{d} x}$ ， $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

求在给定点的导数，我们发现函数的切线斜率为

$-\frac{1}{2-0}=-\frac{1}{2}$

然而，我们想要的直线的斜率垂直于这个，所以取负倒数

m=2

现在我们可以用点斜式来表示直线的方程

y-0=2(x-2)

y=2x-4

报告错误

示例问题161:衍生品

求f(x)曲线的切线斜率 x=-2 。四舍五入到最近的整数。

f(x)=16e^x+12x^6-48x+13

可能的答案:

无法从所提供的信息中确定。

2304

正确答案:

解释：

求f(x)曲线的切线斜率 x=-2

f(x)=16e^x+12x^6-48x+13

为了求出切线的斜率，我们需要求出一阶导数。

为了求导数，我们需要回顾两个规则。

$\frac{dy}{dx}e^x=e^x$

和

$\frac{dy}{dx}x^n=nx^{n-1}$

利用这两条法则，我们可以求出f(x)的导数。

第一项可以用第一条规则推导出来。e ^ x的导数就是e ^ x。

这意味着第一项仍然是16e ^ x。

对于其他三项，我们遵循第二条规则。我们将每一项的指数减1，然后将系数乘以原来的指数。

$f'(x)=16e^x+(6)12x^{6-1}-(1)48x^{1-1}$

注意，13将会退出。它是一个常数项，因此当我们把它乘以它原来的指数(0)它也会化为零。

清理上面得到:

$f'(x)=16e^x+72x^{5}-48$

现在，我们就快到了。要求出x=-2时的斜率。为此，将-2代入x求解。

$f'(x)=16e^{-2}+72(-2)^{5}-48\approx -2349.83$

所以答案是-2350

报告错误

问题67:A点导数

求出经过原点并垂直于正切的直线的方程 $x=\frac{\pi}{12}$ ：

$f=\frac{\cos(3x)}{3}$

可能的答案:

$y=\sqrt{2}x$

y=x

$y=-\sqrt{2}x$

$y=-\frac{\sqrt{2}x}{2}$

正确答案:

$y=\sqrt{2}x$

解释：

要确定直线的方程，我们必须先求出它的斜率，也就是垂直的与函数的切线之比。函数在任意点的切线由函数的一阶导数给出:

$f'=\frac{-3\sin(3x)}{3}=-\sin(3x)$

一阶导数是用以下规则求出来的:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ ， $\frac{\mathrm{d} }{\mathrm{d} x} \cos(x)=-\sin(x)$ ， $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

对给定点求导，得到

$-\sin(\frac{\pi}{4})=-\frac{\sqrt{2}}{2}$

因为我们要求的直线的斜率垂直于这条直线，它的斜率是负倒数，或者

$\frac{2}{\sqrt{2}}=\sqrt{2}=m$

现在我们可以用点斜式求直线方程:

$y-0=\sqrt{2}(x-0)$

$y=\sqrt{2}x$

报告错误

问题68:A点导数

求斜率，的, f(x) 在 x=2 ？

f(x)=2x^5-x^3+4

可能的答案:

m=0

m=136

m=148

m=164

m=128

正确答案:

m=148

解释：

函数上任意一点的斜率可以通过将该点的x值代入 f'(x) 的一阶导数 f(x) 。

f(x)=2x^5-x^3+4

f'(x)=10x^4-3x^2

f'(2)=10(2)^4-3(2)^2

=10(16)-3(4)=160-12=148

报告错误

问题51:曲线在一点处的斜率

找到m y = mx + b 从方程中，给定点(2,0)

y = (x^2+2x)(-x^3+4)

可能的答案:

= 144

$= -120$

= -96

= 100

= 48

正确答案:

$= -120$

解释：

为了求出给定点处的切线，我们需要先对给定函数求导。

为了求导数，我们需要用乘法法则。乘积法则说我们取第一个函数的导数乘以第二个函数的导数然后加上第二个函数的导数乘以给定的第一个函数。为了求每个单独函数的导数，我们需要使用幂次法则。

f(x)g'(x)+g(x)f'(x)

幂法则说的是我们取x的指数然后把它放到前面。然后指数减去1

$n(x^{n-1})$

f(x)= x^2 + 2x ; f'(x)= 2x + 2

g(x)= -x^3 +4 ; g'(x) = -3x^2

利用幂法则，我们得到:

(x^2+2x)(-3x^2)+(-x^3+4)(2x+2)

从这里开始，求出给定点处的斜率我们把x代入2。

$(2^2 + 2(2))(-3(2^2)) + (- (2^3)+4)(2(2)+2)$

结果等于 $-120$

报告错误

问题1:对连续性的直观理解

下列哪个函数包含可去除的不连续?

可能的答案:

$f(x)=x^{2}\sin x^{2}$

$f(x)=1-(\ln x)^{2}$

$f(x)=\frac{1+x^{3}}{1+x}$

$f(x)=\frac{x}{1-x^{2}}$

$f(x)=\frac{x+1}{1+x^{2}}$

正确答案:

$f(x)=\frac{1+x^{3}}{1+x}$

解释：

当图中有一个洞可以通过填充一个点来固定(或“移除”)时，就会出现可移除的不连续。换句话说，如果在 x=a ，则极限为方法存在，只是价值 f(a) 没有。

例如，函数 $f (x) = \压裂{1 + x ^ 3} {1 + x}$ 包含可移除的不连续点 x=-1 。注意，我们可以化简 f(x) 如下:

$f (x) = \压裂{1 + x ^ 3} {1 + x} = \压裂{(1 + x) (x ^ 2 x + 1)} {1 + x} = x ^ {2} - x + 1$ ,在那里 $x \ neq 1$ 。

因此，我们可以说 $\ lim_ {x \ rightarrow 1} \压裂{1 + x ^ 3} {1 + x} = \ lim_ {x} \ rightarrow 1 x ^ 2 x + 1 = (1) ^ 2 - (1) + 1 = 3$ 。

我们可以看到，的极限 f(x) 存在于 x=-1 即使，即使 f(-1) 是未定义的。

这意味着 f(x) 会像带方程的抛物线吗 $x ^ {2} - x + 1$ 除非 x=-1 ，图中会有一个洞。然而，如果我们只是定义 f(-1)=3 ，那么我们就可以“消除”这种不连续。因此，我们可以说在点处存在可去除的不连续 x=-1 。

的函数

$f(x)=\frac{x}{1-x^{2}}$ ,

$f(x)=1-(\ln x)^{2}$

有不连续点，但这些不连续点出现在垂直渐近线上，而不是孔洞，因此不能被认为是可去除的。

的函数

$f(x)=x^{2}\sin x^{2}$ 和 $f (x) = \压裂{x + 1} {1 + x ^ {2}}$ 的所有实值是连续的吗;它们没有任何形式的间断。

答案是

$f(x)=\frac{1+x^{3}}{1+x}$ 。

报告错误

问题1:从图表和数值表的大致变化率

$\begin{align*}&\text{Approximate a forward derivative at }x=4\\&\text{Using the following table:}\\&x&&f(x)\\&1&&5\\&4&&-8\\&7&&15\end{align*}$

可能的答案:

$\frac{23}{6}$

$\frac{23}{3}$

$-\frac{8}{3}$

$-\frac{13}{3}$

正确答案:

$\frac{23}{3}$

解释：

$\begin{align*}&\text{To find a forward derivative approximation, we consider function}\\&\text{two values: one at the point of interest and another succeeding}\\&\text{it, and finally that distance between the two. Mathematically,}\\&\text{this follows the form:}\\&f'(x)=\frac{f(x+h)-f(x)}{h}\\&\text{Where h is the size of the increment between points on the x-axis.}\\&\text{In approximating a derivative, it is generally prudent to minimize}\\&\text{the distance between function values. In other words, it’s a}\\&\text{good idea to look at two adjacent points. For our problem, that’d}\\&\text{be:}\\&f(4)\text{ and }f(7)\\&\text{Applying the formula above, with }h=3\text{, we find:}\\&f'(4)\approx\frac{15-(15)}{3}\\&f'(4)\approx\frac{23}{3}\end{align*}$

报告错误

←之前 1 2 3. 4 5 6 7 8 9 10 11 12 下一个→

查看AP微积分AB导师

不
认证导师

路易斯堡学院，学士，数学，地质学。弗吉尼亚理工学院和州立大学，地球科学博士。

查看AP微积分AB导师

Damion
认证导师

圣爱德华大学会计学学士。德克萨斯大学奥斯汀分校，会计学硕士。

查看AP微积分AB导师

尼娜
认证导师

普林斯顿大学，计算机科学学士学位。

所有AP微积分AB资源

3诊断测试 164练习题今日问题抽认卡概念学习

受欢迎的科目

MCAT导师在华盛顿特区，芝加哥的ACT导师，迈阿密的LSAT辅导老师，芝加哥LSAT辅导老师，洛杉矶的ACT导师，迈阿密的统计学导师，波士顿的数学导师，芝加哥的生物导师，圣地亚哥的化学导师，圣地亚哥的物理导师

流行备考

在丹佛的ACT考试准备，MCAT考试准备在华盛顿特区，GRE考试准备在旧金山湾区，在圣地亚哥LSAT考试准备，达拉斯沃斯堡GMAT考试准备，凤凰城LSAT考试准备，洛杉矶的ISEE考试准备，芝加哥的SSAT考试准备，波士顿的ACT考试准备，SSAT考试准备在洛杉矶

DMCA的抱怨

如果您认为通过本网站提供的内容(定义见我们的服务条款)侵犯了您的一项或多项版权，请向下列指定代理提供包含以下信息的书面通知(“侵权通知”)。如果Varsity Tutors针对侵权通知采取行动，则将善意地尝试通过该方提供给Varsity Tutors的最新电子邮件地址(如果有的话)联系提供此类内容的一方。

您的侵权通知可能会转发给提供内容的一方或第三方，如ChillingEffects.org。

请注意，如果您对产品或活动侵犯了您的版权做出重大虚假陈述，您将承担损害赔偿责任(包括成本和律师费)。因此，如果您不确定网站上的内容或链接的内容侵犯了您的版权，您应该首先考虑联系律师。

请按照以下步骤提交通知:

你必须包括以下内容:

版权所有人或被授权代表其行事的人的物理或电子签名;对被主张侵犯的版权的认定;对您声称侵犯您版权的内容的性质和确切位置的描述，并提供足够的细节，以便大学导师能够找到并积极识别该内容;例如，我们需要一个特定问题的链接(不仅仅是问题的名称)，其中包含问题的内容和描述-图像，链接，文本等-您的投诉涉及的特定部分;您的姓名、地址、电话号码和电子邮件地址;您的声明:(A)您真诚地相信，使用您声称侵犯您版权的内容未经法律授权，或未经版权所有者或其代理人授权;(b)您的侵权通知中包含的所有信息都是准确的，并且(c)在伪证罪的处罚下，您是版权所有者或被授权代表其行事的人。

向我们的指定代理投诉:

Charles Cohn Varsity Tutors LLC
汉利路101号，300室
圣路易斯，密苏里州63105

或填写以下表格:

不填这个栏

联系信息

＊法定全称

公司名称

＊电话号码

＊电子邮件地址

地址

＊Address1

Address2

＊城市

＊状态

＊Zipcode

＊国家

投诉细节

你所代表的版权持有人(如果不是你本人)

＊版权作品的URL(你的原始材料所在的位置)

＊请说明受版权保护的作品，以便于辨认

我是据称受到侵犯的专有权的所有者，或被授权代表所有者行事的代理人。

这份通知是准确的。

我承认，使用此程序进行虚假或恶意的版权侵权指控可能会产生不利的法律后果。

＊签名(您的数字签名具有法律约束力)

高中

研究生院

学习

搜索50+测试

数学辅导

科学辅导

外语

小学辅导

其他

搜索350+主题

AP微积分AB:点上的导数

学习AP微积分AB的概念，示例问题和解释

所有AP微积分AB资源

例子问题

问题62:A点导数

问题63:A点导数

问题64:A点导数

示例问题161:衍生品

示例问题161:衍生品

问题67:A点导数

问题68:A点导数

问题51:曲线在一点处的斜率

问题1:对连续性的直观理解

问题1:从图表和数值表的大致变化率

所有AP微积分AB资源

报告与此问题相关的问题

DMCA的抱怨

联系信息

地址

投诉细节

寻找最好的导师

电子邮件地址:
你的名字:
反馈: