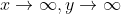例子问题
例子问题1:极值、终端行为和图形对称性
函数的
结束的行为:
局部极大值和极小值:(0,-1)和(-2,3)
对称:既非偶也非奇
结束的行为:
局部极大值和极小值:(0,1)和(2,-3)
对称:既非偶也非奇
结束的行为:
局部极大值和极小值:(0,1)和(2,-3)
对称:既非偶也非奇
结束的行为:
局部极大值和极小值:(0,-1)和(-2,3)
对称:既非偶也非奇
结束的行为:
局部极大值和极小值:(0,1)和(2,-3)
对称:既非偶也非奇
要开始解决这个问题,使用图形计算器或其他图形工具来可视化函数是有帮助的。的图像

当确定最终行为时,你要问自己“当x变得无限大/无限小时,y会发生什么?”如果你从x=0开始,然后向左移动到x=-1,你可以看到y的值越来越小(越来越负)。因此,当x趋于负无穷时,y也趋于负无穷。接下来,看一下x=2 x=3,以此类推,你会发现随着x越来越大,y也越来越大,因此当x趋于无穷时,y也趋于无穷。数学上,这是这样写的:
作为

接下来,问题要求识别任何局部极小值和极大值。我们可以将其视为“高峰”和“低谷”。看一下这个图,它们似乎存在于点(0,1)和(2,-3)处。我们可以通过代入这些x值来进行代数检验,看到相关的y值从函数中出来。
这证实了点(0,1)是局部极大值(峰值),点(2,-3)是局部极小值(谷)。
最后,这个问题要求我们判断图是偶对称、奇对称还是不对称。为了使图形具有均匀的对称性,当它在y轴上反射时必须产生相同的图像。这个图的右边有局部极小值,而左边没有,因此,这个图不是偶的。为了具有奇对称性,图形必须对称于直线y=x。发现这一点的一个简单方法是,看看图表的右边向上和上下颠倒看起来是否一样。因此,这个图形没有对称性。从代数上讲,如果f(x)=f(-x),则函数具有偶对称性;如果-f(x)=f(-x),则函数具有奇对称性。
例子问题2:极值、终端行为和图形对称性
下面是…的图表

选择正确指示此图是偶对称、奇对称还是两者都不对称的选项。
奇怪的对称
不对称
即使是对称
即使是对称
这个问题要求我们判断这个图是偶对称、奇对称还是不对称。为了使图形具有均匀的对称性,当它在y轴上反射时必须产生相同的图像。我们可以看到,直线x=0的左侧与直线x=0的右侧是完全匹配的。因此,这个图具有均匀的对称性。从代数上讲,如果f(x)=f(-x),函数具有偶对称性。您可以插入x的几个测试值来自己查看这一点。
例子问题1:极值、终端行为和图形对称性
下面是…的图表

选择正确指示此图的结束行为的选项。
作为
作为
作为
作为
作为
作为
作为
作为
作为
作为
当确定最终行为时,你要问自己“当x变得无限大/无限小时,y会发生什么?”如果你从x=0开始,然后向左移动到x=-1,你可以看到y的值越来越大(越来越正)。因此,当x趋于负无穷时,y趋于无穷。然后再从原点开始,这次向右移动。可以看到,随着x越来越大,y也越来越大,因此当x趋于无穷时,y也趋于无穷。数学上,这是这样写的:
作为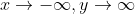

示例问题4:极值、终端行为和图形对称性
下面是…的图表

选择正确指示此图的结束行为的选项。
作为
作为
作为
作为
作为
作为
作为
作为
作为
作为
当确定最终行为时,你要问自己“当x变得无限大/无限小时,y会发生什么?”如果你从x=0开始,然后向左移动到x=-1,你可以看到y的值越来越大(越来越正)。因此,当x趋于负无穷时,y趋于无穷。然后再从原点开始,这次向右移动。可以看到,随着x越来越大,y越来越负。因此,当x趋于无穷时,y趋于负无穷。数学上,这是这样写的:
作为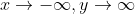

示例问题5:极值、终端行为和图形对称性
下面是…的图表

选择正确指示此图的结束行为的选项。
作为
作为
作为
作为
作为
作为
作为
作为
作为
作为
当确定最终行为时,你要问自己“当x变得无限大/无限小时,y会发生什么?”如果你从x=0开始,然后向左移动到x=-1,你可以看到y的值越来越小(越来越负)。因此,当x趋于负无穷时,y也趋于负无穷。然后再从原点开始,这次向右移动。可以看到,随着x越来越大,y也越来越大,因此当x趋于无穷时,y也趋于无穷。数学上,这是这样写的:
作为

示例问题6:极值、终端行为和图形对称性
下面是…的图表

选择正确指示此图是偶对称、奇对称还是两者都不对称的选项。
这个图有奇对称性。
这个图没有任何对称性。
这个图形具有均匀的对称性。
这个图有奇对称性。
这个问题要求我们判断这个图是偶对称、奇对称还是不对称。为了使图形具有均匀的对称性,当它在y轴上反射时必须产生相同的图像。象限I (x和y都是正的)是图的一部分,而象限II (x为负,y为正)是图的一部分。因为这两个不匹配,所以这个图不是偶数。为了具有奇对称性,图形必须对称于直线y=x。发现这一点的一个简单方法是,看看图表的右边向上和上下颠倒看起来是否一样。它确实有这个性质,所以它有奇对称。从代数上讲,如果f(x)=f(-x),则函数具有偶对称性;如果-f(x)=f(-x),则函数具有奇对称性。您可以插入x的几个测试值来自己查看这一点。
示例问题7:极值、终端行为和图形对称性
下面是…的图表

选择正确指示此图是偶对称、奇对称还是两者都不对称的选项。
这个图没有对称性。
这个图有奇对称性。
这个图形具有均匀的对称性。
这个图没有对称性。
这个问题要求我们判断这个图是偶对称、奇对称还是不对称。为了使图形具有均匀的对称性,当它在y轴上反射时必须产生相同的图像。象限I (x和y都为正)和象限II (x为负,y为正)有一部分图;然而,这些作品并不是彼此的镜像。因此,这个图不是偶数的。为了具有奇对称性,图形必须对称于直线y=x。发现这一点的一个简单方法是,看看图表的右边向上和上下颠倒看起来是否一样。在原图中,曲线在原点上方变平,但如果我们把它倒过来,它在原点以下变平。虽然它在点(0,5)周围有奇对称性,但它在原点周围没有对称性,因此函数不是奇函数。因此,这个图没有对称性。 Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x). You can plug in several test values of x to see that neither of these are satisfied.
示例问题8:极值、终端行为和图形对称性
下面是…的图表

选择正确指示此图的结束行为的选项。
作为
作为
作为
作为
作为
作为
作为
作为
作为
作为
当确定最终行为时,你要问自己“当x变得无限大/无限小时,y会发生什么?”如果你从x=0开始,然后向左移动到x=-1,你可以看到y的值越来越小(越来越负)。因此,当x趋于负无穷时,y也趋于负无穷。然后再从原点开始,这次向右移动。可以看到,随着x越来越大,y也越来越大,因此当x趋于无穷时,y也趋于无穷。数学上,这是这样写的:
作为

示例问题9:极值、终端行为和图形对称性
下面是…的图表

选择正确指示此图是偶对称、奇对称还是两者都不对称的选项。
这个图有奇对称性。
这个图没有对称性。
这个图形具有均匀的对称性。
这个图有奇对称性。
这个问题要求我们判断这个图是偶对称、奇对称还是不对称。为了使图形具有均匀的对称性,当它在y轴上反射时必须产生相同的图像。象限I (x和y都为正)没有这个图的一部分,而象限II (x为负,y为正)有这个图的一部分。因为这两个不匹配,所以这个图不是偶数。为了具有奇对称性,图形必须对称于直线y=x。发现这一点的一个简单方法是,看看图表的右边向上和上下颠倒看起来是否一样。它确实有这个性质,所以它有奇对称。从代数上讲,如果f(x)=f(-x),则函数具有偶对称性;如果-f(x)=f(-x),则函数具有奇对称性。您可以插入x的几个测试值来自己查看这一点。