我们首先尝试使用有理根定理来寻找任何有理根，该定理指出，可能的有理根是可能的小数组合的正或负版本，这种组合由分子上的常数项的因子和分母上的前导系数的因子组成。

这句话里的词汇太多了，我们来分解一下。我们从多项式开始。

常数项是没有变量的项(只是一个普通的数字)。在我们的例子中，常数是60。60的可能因数是多少?

前导系数是变量最大次幂前的数。当这些项按降序排列(从最高幂到最低幂)时，前面的系数总是第一个数字。在我们的例子中，领先系数很难被发现。因为前面没有号码，系数默认为1。

这很好，因为唯一的因子是1。1.

然后我们创建所有可能的分数，分子是常数的因数，分母是前导系数的因数。这实际上并没有那么糟糕因为我们唯一可能的分母是1。任何分母为1的分数都只是分子。因此，我们可能的“分数”很简单

然而，我们必须考虑它们的正反两种形式，所以我们最终可能的有理根列表是

不幸的是，这就是这个过程(至少没有图形计算器的帮助)变得不那么有趣的地方。使用合成除法，我们必须尝试每一个可能的根，直到我们成功。没有一致的规则告诉我们从哪里开始。一般来说，从较小的整数开始是最好的，因为综合除法比较容易。因此，我们可以从然后继续等。

为了使这个解释尽可能简短，我将直接跳到第2部分，在第2部分我们将首先发现成功。

因此，2是根。但是，检查一个根是否实际上是一个二重根(它可以工作两次)总是很重要的。因此，让我们再试一次。

2实际上起了两次作用，因此是二重根。因为我们只剩下三项了，我们可以把合成表达式转换回代数表达式。

我们可以因式分解。

把√2写成代数表达式．因为有二重根，我们需要两个。因此，最后的因式是。

展开和简化给了我们它可以恰当地用标准形式表示右边是常数。下面是展开和简化的演练(包括二项式和三项式展开技术)。

记住要将一个多项式中的每一项与另一个多项式中的每一项相乘。

要将这个多项式表示为线性因子的乘积，你必须通过选择的方法找到多项式的零点，然后将得到这些零点的线性表达式组合起来。

因式分解会让你，然后你就剩下对三次多项式进行排序了。我们可以快速地对多项式进行综合除法通过它潜在的根源的因素．这是．

我们知道是0，然后除以原来的多项式而且给出了多项式．我们可以因式分解或者用二次公式．

这样我们就得到了构成多项式的四个线性表达式:

因为5是单根7是二根，多项式的次数是3，所以多项式是．用展开形式表示:

使用分组:对常用术语进行分解的分组:

因此，两个实根来自而且．

使用分组方法分解常用术语:

用分组法将常用术语因式分解:

首先提出公因式2，然后因式分解:

使用分组分解常用术语:

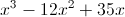
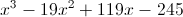
首先，提出公因式，然后因式分解: