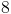The equation of a circle is, in which (h, k) is the center of the circle and r is its radius. Because the graph of the circle is centered at (0, 0), h and k are both 0. Because the radius is 3, the right side of the equation is equal to 9.

The equation of a circle is, in which (h, k) is the center of the circle and r is its radius. Because the graph of the circle is centered at (2, -3), h and k are -2 and 3. Because the radius is 4, the right side of the equation is equal to 16.

The formula for a circle of radius, centered at the pointis given by the general equation:

In this case, the radius is the square root of, which is six, and the center is at

The standard equation for a circle is:

Therefore, the radius is 6 and the center is located at (0,-2)

To find the center or the radius of a circle, first put the equation in the standard form for a circle:, whereis the radius andis the center.

From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula.

, so.

and, soand.

Therefore,.

Because the constant, in this case 4, was not in the original equation, we need to add it to both sides:

Now we do the same for:

We can now find:

To find the center or the radius of a circle, first put the equation in standard form:, whereis the radius andis the center.

From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula.

, so.

and, soand.

This gives.

因为常数,在这种情况下,并不在the original equation, we must add it to both sides:

Now we do the same for:

We can now find the center: (3, -9)

Remember that the "shifts" involved with circular functions are sort of like those found in parabolas. When you shift a parabola left or right, you have to think "oppositely". A right shift requires you to subtract from the x-component, and a left one requires you to add. Hence, this circle has no horizontal shift, but does shift 6 upward for the vertical component.

你也可以记住词的一般公式rcle with center atand a radius of.

比较this to the given equation, we can determine the center point.

The center point is at (0,6) and the circle has a radius of 5.

Remember that the shifts for circles work in an opposite manner from what you might think. They are like the parabola's x-component. Hence, a subtracted variable actually means a shift up or to the right, for the vertical and horizontal components respectively. Since the x-component has a "+5", it is shifted left 5. Since the y-component has a, it is shifted upward 12. Therefore, this circle has a center at.

你也可以记住词的一般公式rcle with center atand a radius of.

比较this to the given equation, we can determine the center point.

The center point is atand the circle has a radius of 6.

Remember that for the equation of a circle, the lone number to the right of the equals sign is the radius squared.

The general formula for a circle with center atand a radius ofis:

比较this to the given equation, we can determine the radius.

The center point is atand the circle has a radius of 9.

Remember that the "shifts" involved with circular functions are sort of like those found in parabolas. When you shift a parabola left or right, you have to think "oppositely". A right shift requires you to subtract from the x-component, and a left one requires you to add. Hence, this circle has a positive 3 horizontal shift, and a negative 2 vertical shift.

你也可以记住词的一般公式rcle with center atand a radius of.

比较this to the given equation, we can determine the radius and center point.

The center point is atand the circle has a radius of 7.

The question asks us for the sum of these components: