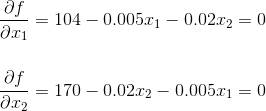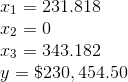例子问题
例子问题1:数学建模
一家美容用品公司生产各种刷子。质量控制工程师的工作是确保在出厂前检测出有缺陷的刷子。据估计,大约有0.2%的刷子会有缺陷。可以对刷子单独进行测试,也可以对刷子批量进行测试。如果对一批笔刷的测试失败,这意味着该特定批中的一个或多个笔刷有缺陷。估计每把刷子的成本是4美分,而且

通过以20个为一组进行测试,可以在不牺牲质量的情况下降低测试成本。
通过以15个为一组的刷子批次进行测试,可以在不牺牲质量的情况下降低测试成本。
通过以9个为一组进行测试,可以在不牺牲质量的情况下降低测试成本。
通过以10个为一组进行测试,可以在不牺牲质量的情况下降低测试成本。
通过以12个为一组进行测试,可以在不牺牲质量的情况下降低测试成本。
通过以15个为一组的刷子批次进行测试,可以在不牺牲质量的情况下降低测试成本。
首先确定已知变量和假设。
如果
如果测试了一批刷子,如果测试显示所有的刷子都是好的,那么,
如果批量测试显示批次中有一个有缺陷的刷子,那么,
使用离散概率模型,找出成本影响最大的质量控制程序,以检测有缺陷的刷子。
考虑随机变量
它的概率是
如果画笔是好的概率是


现在有



因此随机变量的期望值
因此,平均测试成本为,
利用大数定律最小化
现在回答问题。
通过以15个为一组的刷子批次进行测试,可以在不牺牲质量的情况下降低测试成本。
例子问题2:数学建模
一个小镇上游12公里处的一家工厂发生了石油泄漏。泄漏发生一小时后,石油到达溪流,1600米长的油污开始以每小时2公里的速度流向城镇。油在水中的最大浓度是可接受水平的15倍。镇上预计的最大浓度是多少,什么时候到达?
确定已知的和假设。
这是一个扩散问题,因此将使用带有相对浓度项的扩散方程。
相对浓度表示为
这个函数已经规范化,结果如下。
质量守恒定律也将有助于解决这个问题。
目标是计算出城镇的最大污染水平。
扩散方程是,
利用傅里叶变换求解扩散方程如下。
对于这个函数
所以区间是
计算
现在找出最大值在时间上的位置。
例子问题1:马尔可夫链和过程
一家电脑公司只有一名维修人员,在店里可以同时放29台电脑。去年,该店维修了67台电脑,平均每台电脑的维修时间为2天。的马尔可夫过程模型


用马尔科夫过程来解决这个问题,假设空间是有限的。
从概率的角度决定过程未来的随机过程定义如下。
让
回想一下指数分布,因此
现在为这个问题设计一个马尔可夫过程。
电脑进出商店的转变是,


现在计算上下速率。
计算

关键是要知道,在0时,我们不能向下移动一个状态,同样地,在29时,我们不能向上移动一个状态。
解决与
以这种方式继续下去会导致以下结果。
写出有限几何级数的和
现在
因此,
接下来,
例子问题2:马尔可夫链和过程
一家电脑公司只有一名维修人员,在店里可以同时放32台电脑。去年,该店维修了71台电脑,平均每台电脑的维修时间为3天。的马尔可夫过程模型


用马尔科夫过程来解决这个问题,假设空间是有限的。
从概率的角度决定过程未来的随机过程定义如下。
让
回想一下指数分布,因此
现在为这个问题设计一个马尔可夫过程。
电脑进出商店的转变是,


现在计算上下速率。
计算

关键是要知道,在0时,我们不能向下移动一个状态,同样地,在29时,我们不能向上移动一个状态。
解决与
以这种方式继续下去会导致以下结果。
写出有限几何级数的和
现在
因此,
接下来,
例子问题3:马尔可夫链和过程
一家电脑公司只有一名维修人员,在店里同时有23台电脑的空间。去年,该店维修了51台电脑,平均每台电脑的维修时间为5天。的马尔可夫过程模型


用马尔科夫过程来解决这个问题,假设空间是有限的。
从概率的角度决定过程未来的随机过程定义如下。
让
回想一下指数分布,因此
现在为这个问题设计一个马尔可夫过程。
电脑进出商店的转变是,


现在计算上下速率。
计算

关键是要知道,在0时,我们不能向下移动一个状态,同样地,在29时,我们不能向上移动一个状态。
解决与
以这种方式继续下去会导致以下结果。
写出有限几何级数的和
现在
因此,
接下来,
例子问题1:5步骤方法
一头175磅重的奶牛每天增重3磅,饲养这头奶牛每天要花费30美分。牛的市场价格是每磅75美分,但价格正在以每天1美分的速度下降。什么时候卖牛才能获得最大的利润?
使用5步法。
牛应该在4天后出售。
牛应该在2天后出售。
最大利润是131.58美元。
奶牛应该在3天后出售。
最大利润是151.58美元。
奶牛应该在3天后出售。
这个特殊的建模问题的5步方法如下所示。
1.问问题
什么时候卖牛才能获得最大的利润?
现在确定所有已知的信息。
变量:
2.选择建模方法
对于这个特殊的问题,函数是可以定义的

3.制定模型
最大化

现在把方程写成
4.求解模型
现在要解这个模型,求导,令它等于0,然后解
5.回答问题
奶牛应该在3天后出售。
例子问题1:多变量的优化
一家生产电脑显示器的公司将在今年春天推出两款新产品,一款15英寸的屏幕售价189美元,另一款19英寸的屏幕售价269美元。15英寸屏幕的生产成本为85美元/块,19英寸屏幕的生产成本为99美元/块,另外还有20万美元的杂项成本。每种屏幕类型的销售数量影响平均销售价格。据估计,每多卖出一块屏幕,每套产品的平均售价就会下降2美分。15英寸屏幕的平均售价每销售一块19英寸屏幕降低0.2美分,19英寸屏幕每销售一块15英寸屏幕降低0.3美分。用什么偏微分方程来找出每种类型的屏幕应该生产多少单元来优化利润?
首先,确定所有已知的信息。
变量:
假设:
摘要目的:
最大化利润。
定理:如果





因此,要找到该函数中的最大值点,需要同时求解所述微分方程并检查边界点。
现在转换变量/
在
从这里取每个变量的偏微分方程。由于问题要求的是用于优化利润的偏微分方程,我们可以到此为止。
例子问题1:优化模型
采用牛顿法作为计算方法,对跟踪问题进行优化。
一头175磅重的奶牛每天增重3磅,饲养这头奶牛每天要花费30美分。牛的市场价格是每磅75美分,但价格正在以每天1美分的速度下降。什么时候卖牛才能获得最大的利润?
建议等待6 ~ 7天再出售。这将带来130美元的净利润。
建议等9 ~ 10天再卖。这将带来132美元的净利润。
建议等7、8天再卖。这将带来131.90美元的净利润。
建议等8、9天再卖。这将带来132.90美元的净利润。
建议等待2 ~ 5天再出售。这将带来131.90美元的净利润。
建议等7、8天再卖。这将带来131.90美元的净利润。
假设牛的生长速度与它的体重成正比。
用数学术语来说:
看看已知的信息,
变量:
因此,
当
因此要解的微分方程
通过分离变量求解,得到如下公式。
从这里开始,用新的权重方程建立模型。
回想一下,我们的目标是优化问题

使用图形计算器或计算机技术来绘制函数。

观察图表,似乎奶牛的最大利润出现在附近

从这里开始,回答问题。考虑到牛的生长速度还在增加,建议等7、8天再卖牛。这将带来131.90美元的净利润。
例子问题1:线性规划
一个农场有750英亩土地可用于种植作物。可能的作物有大豆、玉米和燕麦。农场有1200英亩英尺的灌溉用水,工人每周可以在农场工作575个小时。
找出每一种作物的种植数量,以使利润最大化。
下表包含了一些额外的有用信息。
这个特殊问题的目标是利润最大化。
功能最大化:
在由约束条件定义的区域上。
首先确定问题的变量和假设。
现在利用约束条件来建立线性规划模型。
从这里用计算机实现用单纯形法求解。
因此,最优的解决方案是种植510英亩大豆和65英亩燕麦。
这个解决方案的最大利润将是223,500美元。
例子问题2:线性规划
一个农场有750英亩土地可用于种植作物。可能的作物有大豆、玉米和燕麦。农场有1200英亩英尺的灌溉用水,工人每周可以在农场工作575个小时。
找出每一种作物的种植数量,以使利润最大化。
下表包含了一些额外的有用信息。
这个特殊问题的目标是利润最大化。
功能最大化:
在由约束条件定义的区域上。
首先确定问题的变量和假设。
现在利用约束条件来建立线性规划模型。
从这里用计算机实现用单纯形法求解。
因此,最优解出现在大豆种植面积343.182英亩,玉米种植面积231.818英亩时。
这个解决方案的最大利润将是$230,454.50。









](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012889/gif.latex)
 \\EC=(3+n)+4n(1-0.998^n) \\EC=3+5n-4n(0.998^n)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1012895/gif.latex)



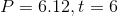
















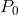














![[\text{Rate In}]=[\text{Rate Out}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1013040/gif.latex)