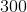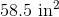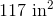In order to solve this equation we need to isolate the variable to one side. Do not forget to perform the same operation on both sides of the equation.

Divide each side of the equation by:

Solve.

Since there are fourteen fewer pounds of Hazelnut Happiness beans in the mixture than Pecan Delight beans , then the number of pounds of Hazelnut Happiness beans is fourteen subtracted from:

.

Add the number of pounds of Pecan Delight beans,, to the number of pounds of Hazelnut Happiness beans,,得到混合物,英镑的数量范围h is.

This translates to the following equation:

When expanding an exponent, we multiply the base by itself for the number indicated by the exponential value.

In this case, our base number isand our exponential value is. So we multiplyby itselftimes.

Remember, the question asks us for the multiplication problem, not the answer to. Because of this,is our correct answer.

In order to solve this problem we need to create a ratio with the given information. It says that for everyvotes cast for candidate A, candidate B gotvote. We can write the following ratio.

现在在给定的数字代替。

We know that candidate B receivedvotes. Write a new ratio.

Now, use the original relationship to create a proportion and solve for the number of votes that candidate A received.

Cross multiply and solve for.

Simplify and solve.

The distributive property can be used to rewrite an expression. When we use this property we will identify and pull out the greatest common factor of each of the addends. Then we can create a quantity that represents the sum of two whole numbers with no common factor multiplied by their greatest common factor.

In this case, the greatest common factor shared by each number is:

After we reduce each addend by the greatest common factor we can rewrite the expression:

We can use substitution to determine which value ofmakes the inequality true.

Because we are looking for a value ofthat makes the expression less than, all of our choices are correct.

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.

First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:

Substitute in our side lengths.

Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by.

Thus, the area formula for a right triangle is as follows:

or

The formula used to find volume of a rectangular prism is as follows:

Substitute our side lengths:

Remember, volume is always written with cubic units because volume is how many cubic units can fit inside of a figure.

In order to solve this question, we need to first recall how to find the area of a rectangle.

Substitute in the given values in the equation and solve for.

Divide both sides by

Dividing by a fraction is the same as multiplying by its inverse or reciprocal.

Find the reciprocal of

Simplify and rewrite.

Multiply and solve.

Reduce.

The width of the fracking site is

First order the numbers from least to greatest:

Then subtract the smallest number from the largest number:

Answer: