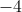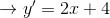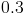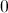例子问题
例子问题1:确定某一点的斜率
求出切线的斜率
求抛物线切线在某一点的斜率,求抛物线方程的导数,然后代入
在这种情况下,在求导之前展开方程是有帮助的:
现在求展开方程的导数:
自
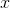



例子问题1:确定绝对极值和局部极值
考虑函数
求函数在区间上的最小值![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90588/gif.latex)
求函数的一阶导数,求函数的潜在最小值
设导数为0:
我们解出

我们可以再检查一下
这意味着函数是凹上的,所以我们找到的点是最小值。
例子问题1:如何找到最大值
的局部最大值是多少

不存在局部最大值。
要找到最大值,我们需要看一阶导数。
为了求一阶导数,我们可以用幂法则。为此,我们将变量的指数降低1,然后乘以原来的指数。
我们要治疗

请注意,
在看一阶导数的时候,记住如果这个方程的输出是正的,原始函数是递增的。如果导数是负的,那么函数是递减的。
请注意,

我们可以用二次方程求根:
因为我们要找的是负数,所以要做减法。
因此,最大值在
例子问题1:图的性质
的局部最大值是多少


这两点之间没有最大值。
为了找到最大值,我们必须找到图从递增到递减的位置。为了找出图表从递增到递减的速率,我们看一下二阶导数,看看值什么时候从正变为负。
也就是说,我们将观察二阶导数,并查看图形与x轴相交的位置(如果有的话)以及从正y值移动到负y值的位置。
现在我们要求二阶导数。不幸的是,三角函数的导数必须记住。一阶导数为:

为了求二阶导数,我们对结果求导。

因此,二阶导数是
我们的新方程是否穿过x轴从正到负




例子问题3:微积分I -导数
的局部最小值是多少

求的局部最小值
为了求一阶导数,我们可以用幂法则。幂法则是指将每个变量乘以其当前指数,然后将该指数降低1。
简化。
任何数的0次方都是1,所以
因此,
至少,我们的

从这里开始,我们分成两个根,一个是加法,一个是减法:
而且
这两个根都满足吗
然后我们转到下一个问题:在这两个根处,图形是否会从负向正平移?是的。当
因此,局部最小值为
问题4:微积分I -导数
的绝对最小值是多少
要找到最小值,我们需要看一阶导数。
因为是相加项,所以对每一部分分别求导。为
记住,
现在我们需要求导数的根。
做


我们的下一个问题是,“在这一点上,图形会从负变为正吗?”是的。这意味着我们的父函数在这一点上已经从递减变成了递增。
因此,这就是最小值。
例子问题2:微积分I -导数
的局部最小值是多少

不存在局部极小值。
局部极小值发生在图形“触底”时——它一直在下降,它减速,停止,然后开始增加。在这一点上,当它从递减变为递增时,一阶导数应该从负变为正。从求一阶导数开始,然后看它是否成立。
求的一阶导数
幂法则是指我们将每个变量乘以其当前指数,然后将每个变量的指数降低1。
自


任何数乘以0都是0,所以最后一项
化简。
那么一阶导数是
画出方程

当0出现时

例子问题1:图的性质
的局部最小值是多少

在这个范围内不存在局部最小值。
y值在这个范围内是常数。
要找到最大值,我们需要看一阶导数。
为了求一阶导数,我们可以用幂法则。为此,我们将变量的指数降低1,然后乘以原来的指数。
我们要治疗

请注意,
在看一阶导数的时候,记住如果这个方程的输出是正的,原始函数是递增的。如果导数是负的,那么函数是递减的。
因为我们想求最小值,我们想知道导数从负到正的变化。
请注意,


例子问题3:微积分I -导数
计算
极限不存在。
替代
(请注意



例子问题1:微积分I -导数
计算
极限不存在。
你可以代入
请注意,