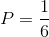例子问题
例子问题1:使用概率做出公平的决定:Ccss.Math.Content.Hss md . b.b 6
劳伦有一项计算机编程任务,要创建一个随机数生成器,在间隔上生成数字![[0,1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/184859/gif.latex)
如果随机数生成器是公平的,那么下列哪个表述必须为真?
在0.5附近产生的数字应该比0或1附近产生的数字多,因为0.5是中位数。
0到1之间的每一个数出现的可能性都是相等的。
在0.5附近产生的数字应该比0或1附近产生的数字多,因为0.5是平均值。
数字0和1不会出现。
0到1之间的每一个数字都有不同的出现概率。
0到1之间的每一个数出现的可能性都是相等的。
例子问题412:高中:统计与概率
职业足球比赛的裁判需要在赛前掷硬币时选择一枚硬币。研究表明,一枚均匀硬币具有以下标准偏差:
他们测试五枚硬币,抛硬币100次,并记录每枚硬币正面或反面落地的次数。根据标准差,下面哪个硬币最不公平?

硬币4
1号和4号硬币
硬币3
2号和5号硬币
硬币1
硬币3
这一标准与我们利用概率做出公平决策的能力有关。其他标准则使用期望均值公式来计算游戏、彩票、保险单、商业投资和其他项目的预期收益。这些信息被用来帮助我们做出是否玩游戏、投资公司或选择保险的决定。同样,这一标准的本质与公平性或使用概率做出公平决策有关。为了回答这个问题,我们需要讨论事件的概率和公平的概念。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这些条件下,我们可以计算出,在“完美世界”中,骰子上的任何数字都应该是六分之一。另一方面,真实或实际的平均值是用“真实”日期计算出来的。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,经过多次滚动,我们最终会发现骰子上的每个数字都有六分之一的机会被滚动。
现在,让我们讨论如何在偶然事件中描述公平。从这个意义上说,公平与随机性有关。这意味着在事件的决定上没有任何偏见。换句话说,在个体方面没有偏见,在用来产生事件结果的设备方面也没有偏见。这意味着由偶然事件产生的决策将是“公平的”。需要注意的是,可能会发生偏离预期概率的情况。例如,一个人可能会在一个公平骰子上连续掷6次6。根据概率,我们预计骰子在六次滚动中只有一次是六面朝上的;然而,偏差的过程可以帮助解释这一现象。
假设我们掷了一个均匀的骰子10次,并记录其分布。接下来,我们决定做无数次。我们将创建一个“钟”形曲线。在这条曲线中,中心将代表可能发生的事件,如平均每6次滚动骰子的每一侧1次。曲线的尾部或极端代表可能发生但极不可能发生的事件,如连续滚动骰子的一侧六次。曲线的死点表示均值,标准差表示在标准条件下,我们可以预期样本偏离均值的程度。换句话说,如果一组骰子多次摇出相同的值,那么我们可以假设它们可能被操纵或改变了。

概率建立在公平和随机性的概念之上。这些术语不一定是同义词。公平与所使用的设备有关(如硬币、纸牌或骰子)。另一方面,随机性是任何统计度量的基本组成部分,它表明每个结果都有相同的发生机会。现在,让我们用这些信息来解题。
为了解决这个问题,我们需要根据标准差计算在标准条件下概率是如何变化的。我们知道抛硬币得到正面或反面的概率是1 / 2;因此,我们可以写出如下的概率:
我们知道标准差等于:
这意味着概率可能会有这个量的变化;因此,一枚均匀硬币可能具有以下概率:
只有一枚硬币拥有超出这个范围的概率:“硬币3”。这枚硬币具有以下概率:
例子问题413:高中:统计与概率
职业足球比赛的裁判需要在赛前掷硬币时选择一枚硬币。研究表明,一枚均匀硬币具有以下标准偏差:
他们测试五枚硬币,抛硬币100次,并记录每枚硬币正面或反面落地的次数。根据标准差,下面哪个硬币最不公平?

硬币3
2号和5号硬币
硬币1
1号和4号硬币
硬币4
硬币3
这一标准与我们利用概率做出公平决策的能力有关。其他标准则使用期望均值公式来计算游戏、彩票、保险单、商业投资和其他项目的预期收益。这些信息被用来帮助我们做出是否玩游戏、投资公司或选择保险的决定。同样,这一标准的本质与公平性或使用概率做出公平决策有关。为了回答这个问题,我们需要讨论事件的概率和公平的概念。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这些条件下,我们可以计算出,在“完美世界”中,骰子上的任何数字都应该是六分之一。另一方面,真实或实际的平均值是用“真实”日期计算出来的。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,经过多次滚动,我们最终会发现骰子上的每个数字都有六分之一的机会被滚动。
现在,让我们讨论如何在偶然事件中描述公平。从这个意义上说,公平与随机性有关。这意味着在事件的决定上没有任何偏见。换句话说,在个体方面没有偏见,在用来产生事件结果的设备方面也没有偏见。这意味着由偶然事件产生的决策将是“公平的”。需要注意的是,可能会发生偏离预期概率的情况。例如,一个人可能会在一个公平骰子上连续掷6次6。根据概率,我们预计骰子在六次滚动中只有一次是六面朝上的;然而,偏差的过程可以帮助解释这一现象。
假设我们掷了一个均匀的骰子10次,并记录其分布。接下来,我们决定做无数次。我们将创建一个“钟”形曲线。在这条曲线中,中心将代表可能发生的事件,如平均每6次滚动骰子的每一侧1次。曲线的尾部或极端代表可能发生但极不可能发生的事件,如连续滚动骰子的一侧六次。曲线的死点表示均值,标准差表示在标准条件下,我们可以预期样本偏离均值的程度。换句话说,如果一组骰子多次摇出相同的值,那么我们可以假设它们可能被操纵或改变了。

概率建立在公平和随机性的概念之上。这些术语不一定是同义词。公平与所使用的设备有关(如硬币、纸牌或骰子)。另一方面,随机性是任何统计度量的基本组成部分,它表明每个结果都有相同的发生机会。现在,让我们用这些信息来解题。
为了解决这个问题,我们需要根据标准差计算在标准条件下概率是如何变化的。我们知道抛硬币得到正面或反面的概率是1 / 2;因此,我们可以写出如下的概率:
我们知道标准差等于:
这意味着概率可能会有这个量的变化;因此,一枚均匀硬币可能具有以下概率:
只有一枚硬币拥有超出这个范围的概率:“硬币3”。这枚硬币具有以下概率:
例子问题414:高中:统计与概率
职业足球比赛的裁判需要在赛前掷硬币时选择一枚硬币。研究表明,一枚均匀硬币具有以下标准偏差:
他们测试五枚硬币,抛硬币100次,并记录每枚硬币正面或反面落地的次数。根据标准差,下列哪个硬币最不公平?
硬币5
硬币1和硬币2
不能确定的
硬币1和硬币4
硬币3和硬币5
硬币5
这一标准与我们利用概率做出公平决策的能力有关。其他标准则使用期望均值公式来计算游戏、彩票、保险单、商业投资和其他项目的预期收益。这些信息被用来帮助我们做出是否玩游戏、投资公司或选择保险的决定。同样,这一标准的本质与公平性或使用概率做出公平决策有关。为了回答这个问题,我们需要讨论事件的概率和公平的概念。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这些条件下,我们可以计算出,在“完美世界”中,骰子上的任何数字都应该是六分之一。另一方面,真实或实际的平均值是用“真实”日期计算出来的。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,经过多次滚动,我们最终会发现骰子上的每个数字都有六分之一的机会被滚动。
现在,让我们讨论如何在偶然事件中描述公平。从这个意义上说,公平与随机性有关。这意味着在事件的决定上没有任何偏见。换句话说,在个体方面没有偏见,在用来产生事件结果的设备方面也没有偏见。这意味着由偶然事件产生的决策将是“公平的”。需要注意的是,可能会发生偏离预期概率的情况。例如,一个人可能会在一个公平骰子上连续掷6次6。根据概率,我们预计骰子在六次滚动中只有一次是六面朝上的;然而,偏差的过程可以帮助解释这一现象。
假设我们掷了一个均匀的骰子10次,并记录其分布。接下来,我们决定做无数次。我们将创建一个“钟”形曲线。在这条曲线中,中心将代表可能发生的事件,如平均每6次滚动骰子的每一侧1次。曲线的尾部或极端代表可能发生但极不可能发生的事件,如连续滚动骰子的一侧六次。曲线的死点表示均值,标准差表示在标准条件下,我们可以预期样本偏离均值的程度。换句话说,如果一组骰子多次摇出相同的值,那么我们可以假设它们可能被操纵或改变了。

概率建立在公平和随机性的概念之上。这些术语不一定是同义词。公平与所使用的设备有关(如硬币、纸牌或骰子)。另一方面,随机性是任何统计度量的基本组成部分,它表明每个结果都有相同的发生机会。现在,让我们用这些信息来解题。
为了解决这个问题,我们需要根据标准差计算在标准条件下概率是如何变化的。我们知道抛硬币得到正面或反面的概率是1 / 2;因此,我们可以写出如下的概率:
我们知道标准差等于:
这意味着概率可能会有这个量的变化;因此,一枚均匀硬币可能具有以下概率:
以下硬币的概率在这个范围之外:,硬币1,硬币2,硬币3,硬币4,硬币5
最不公平的硬币是:硬币5
例子问题415:高中:统计与概率
职业足球比赛的裁判需要在赛前掷硬币时选择一枚硬币。研究表明,一枚均匀硬币具有以下标准偏差:
他们测试五枚硬币,抛硬币100次,并记录每枚硬币正面或反面落地的次数。根据标准差,下列哪个硬币最不公平?
不能确定的
硬币1和硬币2
硬币5
硬币4
硬币1
硬币1
这一标准与我们利用概率做出公平决策的能力有关。其他标准则使用期望均值公式来计算游戏、彩票、保险单、商业投资和其他项目的预期收益。这些信息被用来帮助我们做出是否玩游戏、投资公司或选择保险的决定。同样,这一标准的本质与公平性或使用概率做出公平决策有关。为了回答这个问题,我们需要讨论事件的概率和公平的概念。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这些条件下,我们可以计算出,在“完美世界”中,骰子上的任何数字都应该是六分之一。另一方面,真实或实际的平均值是用“真实”日期计算出来的。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,经过多次滚动,我们最终会发现骰子上的每个数字都有六分之一的机会被滚动。
现在,让我们讨论如何在偶然事件中描述公平。从这个意义上说,公平与随机性有关。这意味着在事件的决定上没有任何偏见。换句话说,在个体方面没有偏见,在用来产生事件结果的设备方面也没有偏见。这意味着由偶然事件产生的决策将是“公平的”。需要注意的是,可能会发生偏离预期概率的情况。例如,一个人可能会在一个公平骰子上连续掷6次6。根据概率,我们预计骰子在六次滚动中只有一次是六面朝上的;然而,偏差的过程可以帮助解释这一现象。
假设我们掷了一个均匀的骰子10次,并记录其分布。接下来,我们决定做无数次。我们将创建一个“钟”形曲线。在这条曲线中,中心将代表可能发生的事件,如平均每6次滚动骰子的每一侧1次。曲线的尾部或极端代表可能发生但极不可能发生的事件,如连续滚动骰子的一侧六次。曲线的死点表示均值,标准差表示在标准条件下,我们可以预期样本偏离均值的程度。换句话说,如果一组骰子多次摇出相同的值,那么我们可以假设它们可能被操纵或改变了。

概率建立在公平和随机性的概念之上。这些术语不一定是同义词。公平与所使用的设备有关(如硬币、纸牌或骰子)。另一方面,随机性是任何统计度量的基本组成部分,它表明每个结果都有相同的发生机会。现在,让我们用这些信息来解题。
为了解决这个问题,我们需要根据标准差计算在标准条件下概率是如何变化的。我们知道抛硬币得到正面或反面的概率是1 / 2;因此,我们可以写出如下的概率:
我们知道标准差等于:
这意味着概率可能会有这个量的变化;因此,一枚均匀硬币可能具有以下概率:
以下硬币的概率在这个范围之外:,硬币1,硬币2,硬币3,硬币4,硬币5
最不公平的硬币是:硬币1
例子问题416:高中:统计与概率
职业足球比赛的裁判需要在赛前掷硬币时选择一枚硬币。研究表明,一枚均匀硬币具有以下标准偏差:
他们测试五枚硬币,抛硬币100次,并记录每枚硬币正面或反面落地的次数。根据标准差,下列哪个硬币最不公平?
不能确定的
硬币2
硬币3
硬币1和硬币4
硬币3和硬币5
硬币3
这一标准与我们利用概率做出公平决策的能力有关。其他标准则使用期望均值公式来计算游戏、彩票、保险单、商业投资和其他项目的预期收益。这些信息被用来帮助我们做出是否玩游戏、投资公司或选择保险的决定。同样,这一标准的本质与公平性或使用概率做出公平决策有关。为了回答这个问题,我们需要讨论事件的概率和公平的概念。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这些条件下,我们可以计算出,在“完美世界”中,骰子上的任何数字都应该是六分之一。另一方面,真实或实际的平均值是用“真实”日期计算出来的。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,经过多次滚动,我们最终会发现骰子上的每个数字都有六分之一的机会被滚动。
现在,让我们讨论如何在偶然事件中描述公平。从这个意义上说,公平与随机性有关。这意味着在事件的决定上没有任何偏见。换句话说,在个体方面没有偏见,在用来产生事件结果的设备方面也没有偏见。这意味着由偶然事件产生的决策将是“公平的”。需要注意的是,可能会发生偏离预期概率的情况。例如,一个人可能会在一个公平骰子上连续掷6次6。根据概率,我们预计骰子在六次滚动中只有一次是六面朝上的;然而,偏差的过程可以帮助解释这一现象。
假设我们掷了一个均匀的骰子10次,并记录其分布。接下来,我们决定做无数次。我们将创建一个“钟”形曲线。在这条曲线中,中心将代表可能发生的事件,如平均每6次滚动骰子的每一侧1次。曲线的尾部或极端代表可能发生但极不可能发生的事件,如连续滚动骰子的一侧六次。曲线的死点表示均值,标准差表示在标准条件下,我们可以预期样本偏离均值的程度。换句话说,如果一组骰子多次摇出相同的值,那么我们可以假设它们可能被操纵或改变了。

概率建立在公平和随机性的概念之上。这些术语不一定是同义词。公平与所使用的设备有关(如硬币、纸牌或骰子)。另一方面,随机性是任何统计度量的基本组成部分,它表明每个结果都有相同的发生机会。现在,让我们用这些信息来解题。
为了解决这个问题,我们需要根据标准差计算在标准条件下概率是如何变化的。我们知道抛硬币得到正面或反面的概率是1 / 2;因此,我们可以写出如下的概率:
我们知道标准差等于:
这意味着概率可能会有这个量的变化;因此,一枚均匀硬币可能具有以下概率:
以下硬币的概率在这个范围之外:,硬币1,硬币3,硬币5
最不公平的硬币是:硬币3
例子问题417:高中:统计与概率
职业足球比赛的裁判需要在赛前掷硬币时选择一枚硬币。研究表明,一枚均匀硬币具有以下标准偏差:
s = 0.02
他们测试五枚硬币,抛硬币100次,并记录每枚硬币正面或反面落地的次数。根据标准差,下列哪个硬币最不公平?
硬币2
不能确定的
硬币1
硬币1和硬币2
硬币4
硬币4
这一标准与我们利用概率做出公平决策的能力有关。其他标准则使用期望均值公式来计算游戏、彩票、保险单、商业投资和其他项目的预期收益。这些信息被用来帮助我们做出是否玩游戏、投资公司或选择保险的决定。同样,这一标准的本质与公平性或使用概率做出公平决策有关。为了回答这个问题,我们需要讨论事件的概率和公平的概念。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这些条件下,我们可以计算出,在“完美世界”中,骰子上的任何数字都应该是六分之一。另一方面,真实或实际的平均值是用“真实”日期计算出来的。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,经过多次滚动,我们最终会发现骰子上的每个数字都有六分之一的机会被滚动。
现在,让我们讨论如何在偶然事件中描述公平。从这个意义上说,公平与随机性有关。这意味着在事件的决定上没有任何偏见。换句话说,在个体方面没有偏见,在用来产生事件结果的设备方面也没有偏见。这意味着由偶然事件产生的决策将是“公平的”。需要注意的是,可能会发生偏离预期概率的情况。例如,一个人可能会在一个公平骰子上连续掷6次6。根据概率,我们预计骰子在六次滚动中只有一次是六面朝上的;然而,偏差的过程可以帮助解释这一现象。
假设我们掷了一个均匀的骰子10次,并记录其分布。接下来,我们决定做无数次。我们将创建一个“钟”形曲线。在这条曲线中,中心将代表可能发生的事件,如平均每6次滚动骰子的每一侧1次。曲线的尾部或极端代表可能发生但极不可能发生的事件,如连续滚动骰子的一侧六次。曲线的死点表示均值,标准差表示在标准条件下,我们可以预期样本偏离均值的程度。换句话说,如果一组骰子多次摇出相同的值,那么我们可以假设它们可能被操纵或改变了。

概率建立在公平和随机性的概念之上。这些术语不一定是同义词。公平与所使用的设备有关(如硬币、纸牌或骰子)。另一方面,随机性是任何统计度量的基本组成部分,它表明每个结果都有相同的发生机会。现在,让我们用这些信息来解题。
为了解决这个问题,我们需要根据标准差计算在标准条件下概率是如何变化的。我们知道抛硬币得到正面或反面的概率是1 / 2;因此,我们可以写出如下的概率:
我们知道标准差等于:
这意味着概率可能会有这个量的变化;因此,一枚均匀硬币可能具有以下概率:
以下硬币的概率在这个范围之外:,硬币1,硬币2,硬币3,硬币4,硬币5
最不公平的硬币是:硬币4
例子问题418:高中:统计与概率
职业足球比赛的裁判需要在赛前掷硬币时选择一枚硬币。研究表明,一枚均匀硬币具有以下标准偏差:
他们测试五枚硬币,抛硬币100次,并记录每枚硬币正面或反面落地的次数。根据标准差,下列哪个硬币最不公平?
硬币5
硬币1和硬币2
硬币4
硬币1和硬币4
硬币3
硬币4
这一标准与我们利用概率做出公平决策的能力有关。其他标准则使用期望均值公式来计算游戏、彩票、保险单、商业投资和其他项目的预期收益。这些信息被用来帮助我们做出是否玩游戏、投资公司或选择保险的决定。同样,这一标准的本质与公平性或使用概率做出公平决策有关。为了回答这个问题,我们需要讨论事件的概率和公平的概念。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这些条件下,我们可以计算出,在“完美世界”中,骰子上的任何数字都应该是六分之一。另一方面,真实或实际的平均值是用“真实”日期计算出来的。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,经过多次滚动,我们最终会发现骰子上的每个数字都有六分之一的机会被滚动。
现在,让我们讨论如何在偶然事件中描述公平。从这个意义上说,公平与随机性有关。这意味着在事件的决定上没有任何偏见。换句话说,在个体方面没有偏见,在用来产生事件结果的设备方面也没有偏见。这意味着由偶然事件产生的决策将是“公平的”。需要注意的是,可能会发生偏离预期概率的情况。例如,一个人可能会在一个公平骰子上连续掷6次6。根据概率,我们预计骰子在六次滚动中只有一次是六面朝上的;然而,偏差的过程可以帮助解释这一现象。
假设我们掷了一个均匀的骰子10次,并记录其分布。接下来,我们决定做无数次。我们将创建一个“钟”形曲线。在这条曲线中,中心将代表可能发生的事件,如平均每6次滚动骰子的每一侧1次。曲线的尾部或极端代表可能发生但极不可能发生的事件,如连续滚动骰子的一侧六次。曲线的死点表示均值,标准差表示在标准条件下,我们可以预期样本偏离均值的程度。换句话说,如果一组骰子多次摇出相同的值,那么我们可以假设它们可能被操纵或改变了。

概率建立在公平和随机性的概念之上。这些术语不一定是同义词。公平与所使用的设备有关(如硬币、纸牌或骰子)。另一方面,随机性是任何统计度量的基本组成部分,它表明每个结果都有相同的发生机会。现在,让我们用这些信息来解题。
为了解决这个问题,我们需要根据标准差计算在标准条件下概率是如何变化的。我们知道抛硬币得到正面或反面的概率是1 / 2;因此,我们可以写出如下的概率:
我们知道标准差等于:
这意味着概率可能会有这个量的变化;因此,一枚均匀硬币可能具有以下概率:
以下硬币的概率在这个范围之外:,硬币1,硬币2,硬币3,硬币4,硬币5
最不公平的硬币是:硬币4
例子问题419:高中:统计与概率
职业足球比赛的裁判需要在赛前掷硬币时选择一枚硬币。研究表明,一枚均匀硬币具有以下标准偏差:
他们测试五枚硬币,抛硬币100次,并记录每枚硬币正面或反面落地的次数。根据标准差,下列哪个硬币最不公平?
硬币3
硬币1
硬币5
硬币2
硬币4
硬币4
这一标准与我们利用概率做出公平决策的能力有关。其他标准则使用期望均值公式来计算游戏、彩票、保险单、商业投资和其他项目的预期收益。这些信息被用来帮助我们做出是否玩游戏、投资公司或选择保险的决定。同样,这一标准的本质与公平性或使用概率做出公平决策有关。为了回答这个问题,我们需要讨论事件的概率和公平的概念。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这些条件下,我们可以计算出,在“完美世界”中,骰子上的任何数字都应该是六分之一。另一方面,真实或实际的平均值是用“真实”日期计算出来的。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,经过多次滚动,我们最终会发现骰子上的每个数字都有六分之一的机会被滚动。
现在,让我们讨论如何在偶然事件中描述公平。从这个意义上说,公平与随机性有关。这意味着在事件的决定上没有任何偏见。换句话说,在个体方面没有偏见,在用来产生事件结果的设备方面也没有偏见。这意味着由偶然事件产生的决策将是“公平的”。需要注意的是,可能会发生偏离预期概率的情况。例如,一个人可能会在一个公平骰子上连续掷6次6。根据概率,我们预计骰子在六次滚动中只有一次是六面朝上的;然而,偏差的过程可以帮助解释这一现象。
假设我们掷了一个均匀的骰子10次,并记录其分布。接下来,我们决定做无数次。我们将创建一个“钟”形曲线。在这条曲线中,中心将代表可能发生的事件,如平均每6次滚动骰子的每一侧1次。曲线的尾部或极端代表可能发生但极不可能发生的事件,如连续滚动骰子的一侧六次。曲线的死点表示均值,标准差表示在标准条件下,我们可以预期样本偏离均值的程度。换句话说,如果一组骰子多次摇出相同的值,那么我们可以假设它们可能被操纵或改变了。

概率建立在公平和随机性的概念之上。这些术语不一定是同义词。公平与所使用的设备有关(如硬币、纸牌或骰子)。另一方面,随机性是任何统计度量的基本组成部分,它表明每个结果都有相同的发生机会。现在,让我们用这些信息来解题。
为了解决这个问题,我们需要根据标准差计算在标准条件下概率是如何变化的。我们知道抛硬币得到正面或反面的概率是1 / 2;因此,我们可以写出如下的概率:
我们知道标准差等于:
这意味着概率可能会有这个量的变化;因此,一枚均匀硬币可能具有以下概率:
以下硬币的概率在这个范围之外:,硬币2,硬币4,硬币5
最不公平的硬币是:硬币4
例子问题81:利用概率来做决定
职业足球比赛的裁判需要在赛前掷硬币时选择一枚硬币。研究表明,一枚均匀硬币具有以下标准偏差:
他们测试五枚硬币,抛硬币100次,并记录每枚硬币正面或反面落地的次数。根据标准差,下列哪个硬币最不公平?
硬币5和硬币2
硬币3和硬币4
硬币4
硬币5
硬币1
硬币1
这一标准与我们利用概率做出公平决策的能力有关。其他标准则使用期望均值公式来计算游戏、彩票、保险单、商业投资和其他项目的预期收益。这些信息被用来帮助我们做出是否玩游戏、投资公司或选择保险的决定。同样,这一标准的本质与公平性或使用概率做出公平决策有关。为了回答这个问题,我们需要讨论事件的概率和公平的概念。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。数学上,我们通过将事件除以样本空间来计算概率:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这些条件下,我们可以计算出,在“完美世界”中,骰子上的任何数字都应该是六分之一。另一方面,真实或实际的平均值是用“真实”日期计算出来的。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,经过多次滚动,我们最终会发现骰子上的每个数字都有六分之一的机会被滚动。
现在,让我们讨论如何在偶然事件中描述公平。从这个意义上说,公平与随机性有关。这意味着在事件的决定上没有任何偏见。换句话说,在个体方面没有偏见,在用来产生事件结果的设备方面也没有偏见。这意味着由偶然事件产生的决策将是“公平的”。需要注意的是,可能会发生偏离预期概率的情况。例如,一个人可能会在一个公平骰子上连续掷6次6。根据概率,我们预计骰子在六次滚动中只有一次是六面朝上的;然而,偏差的过程可以帮助解释这一现象。
假设我们掷了一个均匀的骰子10次,并记录其分布。接下来,我们决定做无数次。我们将创建一个“钟”形曲线。在这条曲线中,中心将代表可能发生的事件,如平均每6次滚动骰子的每一侧1次。曲线的尾部或极端代表可能发生但极不可能发生的事件,如连续滚动骰子的一侧六次。曲线的死点表示均值,标准差表示在标准条件下,我们可以预期样本偏离均值的程度。换句话说,如果一组骰子多次摇出相同的值,那么我们可以假设它们可能被操纵或改变了。

概率建立在公平和随机性的概念之上。这些术语不一定是同义词。公平与所使用的设备有关(如硬币、纸牌或骰子)。另一方面,随机性是任何统计度量的基本组成部分,它表明每个结果都有相同的发生机会。现在,让我们用这些信息来解题。
为了解决这个问题,我们需要根据标准差计算在标准条件下概率是如何变化的。我们知道抛硬币得到正面或反面的概率是1 / 2;因此,我们可以写出如下的概率:
我们知道标准差等于:
这意味着概率可能会有这个量的变化;因此,一枚均匀硬币可能具有以下概率:
以下硬币的概率在这个范围之外:,硬币1,硬币2,硬币4,硬币5
最不公平的硬币是:硬币1