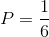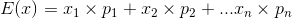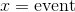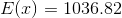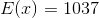例子问题
例子问题51:利用概率来做决定
厄尼有三个赌注可以选。
赌1花费他10美元,赌2花费他15美元,赌3花费他20美元。
支付概率如下:
厄尼应该选哪一个?
押注2
押注3
厄尼不应该接受这三种赌注中的任何一种,因为他都可能赔钱。
押注1
厄尼不应该接受这三种赌注中的任何一种,因为他都可能赔钱。
例子问题57:利用概率来做决定
一名驾车人正试图在以下两项保险中作出选择:

免赔额是指在保险公司支付剩余部分之前,你必须自付的金额。换句话说,如果事故的总成本是



考虑以下:

有了这些信息,我们可以期待哪种政策在下一年能为驾车者节省最多的钱?
高免赔额保单更便宜
不能确定的
低免赔额保单更便宜
低免赔额保单更便宜
高免赔额保单更便宜
高免赔额保单更便宜
这个不合格标准专门与可用于评估和比较与期望值相关的策略相关。这意味着我们将使用我们对概率和期望值的知识来评估各种选择,并做出明智的决定,从长远来看,哪种选择更有利可图。因此,该标准依赖于对概率和预期均值公式的理解。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。用数学方法计算概率事件除以样本空间:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这种情况下我们可以计算任意数量的死在一个“完美世界”应该是6。另一方面,真正的或实际的意思是使用“真实”日期计算。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,在许多卷我们最终会发现每个数字在死滚的六分之十一的概率。
现在,让我们讨论一下如何确定期望平均值。期望平均值的计算公式如下:
在这个方程中,变量被确定为:
我们可以用一个例子来说明这一点。提供了个人和各自尺寸的摩托车立方英寸的列表。如果你要从列表中随机选择一个人,那么你希望他们的摩托车是多大的?

让我们用这些信息来解决这个问题。为了解决摩托车问题,我们需要使用期望平均公式。我们将每个摩托车车主的发动机尺寸替换为其各自的概率并求解。
每个值被选中的概率都是一样的——十一分之一。因此,我们可以化简这个等式:
绕到最近的地方去。
注意,我们可以用这种简化的方式来解决这个问题,因为所有人被选中的概率都是相等的。如果他或她的概率不同,那么我们需要代入每个人各自被选中的概率。
现在,让我们用这些信息来解决问题。我们将使用期望均值公式,代入
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
接下来,我们需要计算与低免赔额保单相关的预期费用。让我们从计算低免赔额保单的主要和次要事故的费用开始。对于轻微事故,损害金额超过免赔额;因此,驾驶者只支付较低的免赔额。同样,在重大事故中,驾驶者只需要支付免赔额;因此,我们可以写出如下公式:
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
最后,我们需要从高免赔额保单中减去低免赔额保单的预期费用,以计算高免赔额保单的便宜程度。
正确的选择如下:
高免赔额保单更便宜
问题58:利用概率来做决定
一名驾车人正试图在以下两项保险中作出选择:

免赔额是指在保险公司支付剩余部分之前,你必须自付的金额。换句话说,如果事故的总成本是



考虑以下:

有了这些信息,我们可以期待哪种政策在下一年能为驾车者节省最多的钱?
高免赔额保单更便宜
不能确定的
低免赔额保单更便宜
低免赔额保单更便宜
高免赔额保单更便宜
高免赔额保单更便宜
这个不合格标准专门与可用于评估和比较与期望值相关的策略相关。这意味着我们将使用我们对概率和期望值的知识来评估各种选择,并做出明智的决定,从长远来看,哪种选择更有利可图。因此,该标准依赖于对概率和预期均值公式的理解。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。用数学方法计算概率事件除以样本空间:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这种情况下我们可以计算任意数量的死在一个“完美世界”应该是6。另一方面,真正的或实际的意思是使用“真实”日期计算。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,在许多卷我们最终会发现每个数字在死滚的六分之十一的概率。
现在,让我们讨论一下如何确定期望平均值。期望平均值的计算公式如下:
在这个方程中,变量被确定为:
我们可以用一个例子来说明这一点。提供了个人和各自尺寸的摩托车立方英寸的列表。如果你要从列表中随机选择一个人,那么你希望他们的摩托车是多大的?

让我们用这些信息来解决这个问题。为了解决摩托车问题,我们需要使用期望平均公式。我们将每个摩托车车主的发动机尺寸替换为其各自的概率并求解。
每个值被选中的概率都是一样的——十一分之一。因此,我们可以化简这个等式:
绕到最近的地方去。
注意,我们可以用这种简化的方式来解决这个问题,因为所有人被选中的概率都是相等的。如果他或她的概率不同,那么我们需要代入每个人各自被选中的概率。
现在,让我们用这些信息来解决问题。我们将使用期望均值公式,代入
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
接下来,我们需要计算与低免赔额保单相关的预期费用。让我们从计算低免赔额保单的主要和次要事故的费用开始。对于轻微事故,损害金额超过免赔额;因此,驾驶者只支付较低的免赔额。同样,在重大事故中,驾驶者只需要支付免赔额;因此,我们可以写出如下公式:
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
最后,我们需要从高免赔额保单中减去低免赔额保单的预期费用,以计算高免赔额保单的便宜程度。
正确的选择如下:
高免赔额保单更便宜
例子问题2:评估和比较期望值策略:Ccss.Math.Content.Hss md . b.b 5b
一名驾车人正试图在以下两项保险中作出选择:
免赔额是指在保险公司支付剩余部分之前,你必须自付的金额。换句话说,如果事故的总成本是



考虑以下:
有了这些信息,我们可以期待哪种政策在下一年能为驾车者节省最多的钱?
高免赔额保单更便宜
不能确定的
低免赔额保单更便宜
低免赔额保单更便宜
高免赔额保单更便宜
低免赔额保单更便宜
这个不合格标准专门与可用于评估和比较与期望值相关的策略相关。这意味着我们将使用我们对概率和期望值的知识来评估各种选择,并做出明智的决定,从长远来看,哪种选择更有利可图。因此,该标准依赖于对概率和预期均值公式的理解。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。用数学方法计算概率事件除以样本空间:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这种情况下我们可以计算任意数量的死在一个“完美世界”应该是6。另一方面,真正的或实际的意思是使用“真实”日期计算。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,在许多卷我们最终会发现每个数字在死滚的六分之十一的概率。
现在,让我们讨论一下如何确定期望平均值。期望平均值的计算公式如下:
在这个方程中,变量被确定为:
我们可以用一个例子来说明这一点。提供了个人和各自尺寸的摩托车立方英寸的列表。如果你要从列表中随机选择一个人,那么你希望他们的摩托车是多大的?

让我们用这些信息来解决这个问题。为了解决摩托车问题,我们需要使用期望平均公式。我们将每个摩托车车主的发动机尺寸替换为其各自的概率并求解。
每个值被选中的概率都是一样的——十一分之一。因此,我们可以化简这个等式:
绕到最近的地方去。
注意,我们可以用这种简化的方式来解决这个问题,因为所有人被选中的概率都是相等的。如果他或她的概率不同,那么我们需要代入每个人各自被选中的概率。
现在,让我们用这些信息来解决问题。我们将使用期望均值公式,代入
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
接下来,我们需要计算与低免赔额保单相关的预期费用。让我们从计算低免赔额保单的主要和次要事故的费用开始。对于轻微事故,损害金额超过免赔额;因此,驾驶者只支付较低的免赔额。同样,在重大事故中,驾驶者只需要支付免赔额;因此,我们可以写出如下公式:
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
最后,我们需要从低免赔额保单中减去高免赔额保单的预期费用,以计算低免赔额保单的便宜程度。
正确的选择如下:
低免赔额保单更便宜
例子问题2:评估和比较期望值策略:Ccss.Math.Content.Hss md . b.b 5b
一名驾车人正试图在以下两项保险中作出选择:
免赔额是指在保险公司支付剩余部分之前,你必须自付的金额。换句话说,如果事故的总成本是



考虑以下:
有了这些信息,我们可以期待哪种政策在下一年能为驾车者节省最多的钱?
高免赔额保单更便宜
高免赔额保单更便宜
低免赔额保单更便宜
低免赔额保单更便宜
不能确定的
低免赔额保单更便宜
这个不合格标准专门与可用于评估和比较与期望值相关的策略相关。这意味着我们将使用我们对概率和期望值的知识来评估各种选择,并做出明智的决定,从长远来看,哪种选择更有利可图。因此,该标准依赖于对概率和预期均值公式的理解。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。用数学方法计算概率事件除以样本空间:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这种情况下我们可以计算任意数量的死在一个“完美世界”应该是6。另一方面,真正的或实际的意思是使用“真实”日期计算。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,在许多卷我们最终会发现每个数字在死滚的六分之十一的概率。
现在,让我们讨论一下如何确定期望平均值。期望平均值的计算公式如下:
在这个方程中,变量被确定为:
我们可以用一个例子来说明这一点。提供了个人和各自尺寸的摩托车立方英寸的列表。如果你要从列表中随机选择一个人,那么你希望他们的摩托车是多大的?

让我们用这些信息来解决这个问题。为了解决摩托车问题,我们需要使用期望平均公式。我们将每个摩托车车主的发动机尺寸替换为其各自的概率并求解。
每个值被选中的概率都是一样的——十一分之一。因此,我们可以化简这个等式:
绕到最近的地方去。
注意,我们可以用这种简化的方式来解决这个问题,因为所有人被选中的概率都是相等的。如果他或她的概率不同,那么我们需要代入每个人各自被选中的概率。
现在,让我们用这些信息来解决问题。我们将使用期望均值公式,代入
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
接下来,我们需要计算与低免赔额保单相关的预期费用。让我们从计算低免赔额保单的主要和次要事故的费用开始。对于轻微事故,损害金额超过免赔额;因此,驾驶者只支付较低的免赔额。同样,在重大事故中,驾驶者只需要支付免赔额;因此,我们可以写出如下公式:
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
E(低\扣除)= \ 1715.0美元
最后,我们需要从低免赔额保单中减去高免赔额保单的预期费用,以计算低免赔额保单的便宜程度。
正确的选择如下:
低免赔额保单更便宜
示例问题3:评估和比较期望值策略:Ccss.Math.Content.Hss md . b.b 5b
一名驾车人正试图在以下两项保险中作出选择:
免赔额是指在保险公司支付剩余部分之前,你必须自付的金额。换句话说,如果事故的总成本是



考虑以下:
有了这些信息,我们可以期待哪种政策在下一年能为驾车者节省最多的钱?
高免赔额保单更便宜
不能确定的
低免赔额保单更便宜
低免赔额保单更便宜
高免赔额保单更便宜
低免赔额保单更便宜
这个不合格标准专门与可用于评估和比较与期望值相关的策略相关。这意味着我们将使用我们对概率和期望值的知识来评估各种选择,并做出明智的决定,从长远来看,哪种选择更有利可图。因此,该标准依赖于对概率和预期均值公式的理解。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。用数学方法计算概率事件除以样本空间:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这种情况下我们可以计算任意数量的死在一个“完美世界”应该是6。另一方面,真正的或实际的意思是使用“真实”日期计算。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,在许多卷我们最终会发现每个数字在死滚的六分之十一的概率。
现在,让我们讨论一下如何确定期望平均值。期望平均值的计算公式如下:
在这个方程中,变量被确定为:
我们可以用一个例子来说明这一点。提供了个人和各自尺寸的摩托车立方英寸的列表。如果你要从列表中随机选择一个人,那么你希望他们的摩托车是多大的?

让我们用这些信息来解决这个问题。为了解决摩托车问题,我们需要使用期望平均公式。我们将每个摩托车车主的发动机尺寸替换为其各自的概率并求解。
每个值被选中的概率都是一样的——十一分之一。因此,我们可以化简这个等式:
绕到最近的地方去。
注意,我们可以用这种简化的方式来解决这个问题,因为所有人被选中的概率都是相等的。如果他或她的概率不同,那么我们需要代入每个人各自被选中的概率。
现在,让我们用这些信息来解决问题。我们将使用期望均值公式,代入
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
接下来,我们需要计算与低免赔额保单相关的预期费用。让我们从计算低免赔额保单的主要和次要事故的费用开始。对于轻微事故,损害金额超过免赔额;因此,驾驶者只支付较低的免赔额。同样,在重大事故中,驾驶者只需要支付免赔额;因此,我们可以写出如下公式:
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
最后,我们需要从低免赔额保单中减去高免赔额保单的预期费用,以计算低免赔额保单的便宜程度。
正确的选择如下:
低免赔额保单更便宜
示例问题4:评估和比较期望值策略:Ccss.Math.Content.Hss md . b.b 5b
一名驾车人正试图在以下两项保险中作出选择:
免赔额是指在保险公司支付剩余部分之前,你必须自付的金额。换句话说,如果事故的总成本是



考虑以下:
有了这些信息,我们可以期待哪种政策在下一年能为驾车者节省最多的钱?
高免赔额保单更便宜
低免赔额保单更便宜
高免赔额保单更便宜
不能确定的
低免赔额保单更便宜
低免赔额保单更便宜
这个不合格标准专门与可用于评估和比较与期望值相关的策略相关。这意味着我们将使用我们对概率和期望值的知识来评估各种选择,并做出明智的决定,从长远来看,哪种选择更有利可图。因此,该标准依赖于对概率和预期均值公式的理解。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。用数学方法计算概率事件除以样本空间:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这种情况下我们可以计算任意数量的死在一个“完美世界”应该是6。另一方面,真正的或实际的意思是使用“真实”日期计算。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,在许多卷我们最终会发现每个数字在死滚的六分之十一的概率。
现在,让我们讨论一下如何确定期望平均值。期望平均值的计算公式如下:
在这个方程中,变量被确定为:
我们可以用一个例子来说明这一点。提供了个人和各自尺寸的摩托车立方英寸的列表。如果你要从列表中随机选择一个人,那么你希望他们的摩托车是多大的?

让我们用这些信息来解决这个问题。为了解决摩托车问题,我们需要使用期望平均公式。我们将每个摩托车车主的发动机尺寸替换为其各自的概率并求解。
每个值被选中的概率都是一样的——十一分之一。因此,我们可以化简这个等式:
绕到最近的地方去。
注意,我们可以用这种简化的方式来解决这个问题,因为所有人被选中的概率都是相等的。如果他或她的概率不同,那么我们需要代入每个人各自被选中的概率。
现在,让我们用这些信息来解决问题。我们将使用期望均值公式,代入
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
接下来,我们需要计算与低免赔额保单相关的预期费用。让我们从计算低免赔额保单的主要和次要事故的费用开始。对于轻微事故,损害金额超过免赔额;因此,驾驶者只支付较低的免赔额。同样,在重大事故中,驾驶者只需要支付免赔额;因此,我们可以写出如下公式:
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
最后,我们需要从低免赔额保单中减去高免赔额保单的预期费用,以计算低免赔额保单的便宜程度。
正确的选择如下:
低免赔额保单更便宜
示例问题5:评估和比较期望值策略:Ccss.Math.Content.Hss md . b.b 5b
一名驾车人正试图在以下两项保险中作出选择:
免赔额是指在保险公司支付剩余部分之前,你必须自付的金额。换句话说,如果事故的总成本是


考虑以下:
有了这些信息,我们可以期待哪种政策在下一年能为驾车者节省最多的钱?
低免赔额保单更便宜
不能确定的
高免赔额保单更便宜
低免赔额保单更便宜
高免赔额保单更便宜
低免赔额保单更便宜
这个不合格标准专门与可用于评估和比较与期望值相关的策略相关。这意味着我们将使用我们对概率和期望值的知识来评估各种选择,并做出明智的决定,从长远来看,哪种选择更有利可图。因此,该标准依赖于对概率和预期均值公式的理解。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。用数学方法计算概率事件除以样本空间:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这种情况下我们可以计算任意数量的死在一个“完美世界”应该是6。另一方面,真正的或实际的意思是使用“真实”日期计算。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,在许多卷我们最终会发现每个数字在死滚的六分之十一的概率。
现在,让我们讨论一下如何确定期望平均值。期望平均值的计算公式如下:
在这个方程中,变量被确定为:
我们可以用一个例子来说明这一点。提供了个人和各自尺寸的摩托车立方英寸的列表。如果你要从列表中随机选择一个人,那么你希望他们的摩托车是多大的?

让我们用这些信息来解决这个问题。为了解决摩托车问题,我们需要使用期望平均公式。我们将每个摩托车车主的发动机尺寸替换为其各自的概率并求解。
每个值被选中的概率都是一样的——十一分之一。因此,我们可以化简这个等式:
绕到最近的地方去。
注意,我们可以用这种简化的方式来解决这个问题,因为所有人被选中的概率都是相等的。如果他或她的概率不同,那么我们需要代入每个人各自被选中的概率。
现在,让我们用这些信息来解决问题。我们将使用期望均值公式,代入
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
接下来,我们需要计算与低免赔额保单相关的预期费用。让我们从计算低免赔额保单的主要和次要事故的费用开始。对于轻微事故,损害金额超过免赔额;因此,驾驶者只支付较低的免赔额。同样,在重大事故中,驾驶者只需要支付免赔额;因此,我们可以写出如下公式:
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
最后,我们需要从低免赔额保单中减去高免赔额保单的预期费用,以计算低免赔额保单的便宜程度。
正确的选择如下:
低免赔额保单更便宜
示例问题6:评估和比较期望值策略:Ccss.Math.Content.Hss md . b.b 5b
一名驾车人正试图在以下两项保险中作出选择:
免赔额是指在保险公司支付剩余部分之前,你必须自付的金额。换句话说,如果事故的总成本是



考虑以下:
有了这些信息,我们可以期待哪种政策在下一年能为驾车者节省最多的钱?
高免赔额保单更便宜
低免赔额保单更便宜
高免赔额保单更便宜
不能确定的
低免赔额保单更便宜
低免赔额保单更便宜
这个不合格标准专门与可用于评估和比较与期望值相关的策略相关。这意味着我们将使用我们对概率和期望值的知识来评估各种选择,并做出明智的决定,从长远来看,哪种选择更有利可图。因此,该标准依赖于对概率和预期均值公式的理解。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。用数学方法计算概率事件除以样本空间:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这种情况下我们可以计算任意数量的死在一个“完美世界”应该是6。另一方面,真正的或实际的意思是使用“真实”日期计算。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,在许多卷我们最终会发现每个数字在死滚的六分之十一的概率。
现在,让我们讨论一下如何确定期望平均值。期望平均值的计算公式如下:
在这个方程中,变量被确定为:
我们可以用一个例子来说明这一点。提供了个人和各自尺寸的摩托车立方英寸的列表。如果你要从列表中随机选择一个人,那么你希望他们的摩托车是多大的?

让我们用这些信息来解决这个问题。为了解决摩托车问题,我们需要使用期望平均公式。我们将每个摩托车车主的发动机尺寸替换为其各自的概率并求解。
每个值被选中的概率都是一样的——十一分之一。因此,我们可以化简这个等式:
绕到最近的地方去。
注意,我们可以用这种简化的方式来解决这个问题,因为所有人被选中的概率都是相等的。如果他或她的概率不同,那么我们需要代入每个人各自被选中的概率。
现在,让我们用这些信息来解决问题。我们将使用期望均值公式,代入
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
接下来,我们需要计算与低免赔额保单相关的预期费用。让我们从计算低免赔额保单的主要和次要事故的费用开始。对于轻微事故,损害金额超过免赔额;因此,驾驶者只支付较低的免赔额。同样,在重大事故中,驾驶者只需要支付免赔额;因此,我们可以写出如下公式:
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
最后,我们需要从低免赔额保单中减去高免赔额保单的预期费用,以计算低免赔额保单的便宜程度。
正确的选择如下:
低免赔额保单更便宜
示例问题7:评估和比较期望值策略:Ccss.Math.Content.Hss md . b.b 5b
一名驾车人正试图在以下两项保险中作出选择:
免赔额是指在保险公司支付剩余部分之前,你必须自付的金额。换句话说,如果事故的总成本是



考虑以下:
有了这些信息,我们可以期待哪种政策在下一年能为驾车者节省最多的钱?
高免赔额保单更便宜
不能确定的
低免赔额保单更便宜
低免赔额保单更便宜
高免赔额保单更便宜
低免赔额保单更便宜
这个不合格标准专门与可用于评估和比较与期望值相关的策略相关。这意味着我们将使用我们对概率和期望值的知识来评估各种选择,并做出明智的决定,从长远来看,哪种选择更有利可图。因此,该标准依赖于对概率和预期均值公式的理解。首先,我们将讨论一般意义上的概率。
概率通常被定义为一个事件发生的机会或可能性。它通过识别两个组成部分来计算:事件和样本空间。事件被定义为我们希望观察到的有利结果或成功。另一方面,样本空间被定义为事件的所有可能结果的集合。用数学方法计算概率事件除以样本空间:
让我们举一个简单的例子:滚动骰子。我们想知道摇到1的概率。我们知道样本空间是6因为骰子有6条边或结果。而且,我们知道只有一条边的值为1;因此,
现在,让我们把它转换成百分比:
用分数形式表示的概率的值在0到1之间。1表示事件一定会发生,0表示事件不会发生。同样,以百分比表示的概率的值在0到100%之间,接近于0的概率不太可能发生,接近于100%的概率更可能发生。
根据这个逻辑,我们期望在骰子上掷一个特定的数字,每六次掷一次;然而,我们可能多次摇同一个数字,或者在六次摇中完全不摇。这种差异造成了预期平均值和实际平均值之间的差异。预期平均值是一种假设计算,假设样本量非常大,且没有中间变量(如辊上的不同力和辊间滚动的模具表面摩擦的变化)。在这种情况下我们可以计算任意数量的死在一个“完美世界”应该是6。另一方面,真正的或实际的意思是使用“真实”日期计算。在这些计算中,我们将掷一个骰子特定的次数,并利用它来开发掷特定次数的概率。值得注意的是,从理论上讲,经过大量或接近无限次的试验,实际均值最终将等于预期均值。换句话说,在许多卷我们最终会发现每个数字在死滚的六分之十一的概率。
现在,让我们讨论一下如何确定期望平均值。期望平均值的计算公式如下:
在这个方程中,变量被确定为:
我们可以用一个例子来说明这一点。提供了个人和各自尺寸的摩托车立方英寸的列表。如果你要从列表中随机选择一个人,那么你希望他们的摩托车是多大的?

让我们用这些信息来解决这个问题。为了解决摩托车问题,我们需要使用期望平均公式。我们将每个摩托车车主的发动机尺寸替换为其各自的概率并求解。
每个值被选中的概率都是一样的——十一分之一。因此,我们可以化简这个等式:
绕到最近的地方去。
注意,我们可以用这种简化的方式来解决这个问题,因为所有人被选中的概率都是相等的。如果他或她的概率不同,那么我们需要代入每个人各自被选中的概率。
现在,让我们用这些信息来解决问题。我们将使用期望均值公式,代入
代入已知值。

现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
接下来,我们需要计算与低免赔额保单相关的预期费用。让我们从计算低免赔额保单的主要和次要事故的费用开始。对于轻微事故,损害金额超过免赔额;因此,驾驶者只支付较低的免赔额。同样,在重大事故中,驾驶者只需要支付免赔额;因此,我们可以写出如下公式:
代入已知值。
解决。
现在,我们需要通过将某一年保单的月支付总和相加,来计算该年的保单总成本。
最后,我们需要从低免赔额保单中减去高免赔额保单的预期费用,以计算低免赔额保单的便宜程度。
正确的选择如下:
低免赔额保单更便宜