例子问题
问题1:体积
假设我要构造一个圆柱形容器。建造两个圆形的两端的成本是每平方英尺5美元,圆形的一面每平方英尺2美元。如果我的预算是100美元,这个集装箱的最大容量是多少?
写出表示圆柱体体积(V)和成本的方程。
我们要求出的值


代入体积方程
所以现在


我们可以用这个
现在我们发现

问题1:地区
我们有这个函数它被用来通过绕直线旋转来形成一个三维图形
.求出那个图形的体积
来
.
体积是无限的
想象一个长度为的测试矩形它是旋转的
形成有面积的圆形圆盘
.圆盘有厚度
所以它的体积是
.为了求出图形的总体积,把它变成一个积分。
执行集成
问题3:如何查找区域的体积
考虑一个高度为H的体积V沿着某个轴,我们简称为H,这样


是什么

体积近似于黎曼和,当我们将n层堆叠在一起时形成
在n变大的极限下,这个表达式变成了积分
问题4:如何查找区域的体积
碗里的体积是多少


自

积分得到:
问题5:如何查找区域的体积
以下功能:
是绕着


注意,对于函数中给定的x值:
f(x)的值是曲线上对应点到x轴之间的距离。如果曲线绕x轴旋转,形成一个三维物体,F (x)可以看作是半径对于任意x值,物体的圆形横截面。
为了定义这个物体的体积,我们可以把它看作是沿着x轴堆叠的无限薄磁盘的总和:
注意这是如何遵循圆柱或圆盘体积的公式的

在哪里

代入函数和值域,可以重写为:
或
积分得到
利用2的上界和0的下界,我们发现,

问题6:如何查找区域的体积
确定边界区域的体积


在边界的区域

确定哪个函数是最上面的函数。这将是大半径,小半径由底部曲线表示。积分的边界在两个有界函数的交点处。求积分。
问题7:如何查找区域的体积
单位圆由




单位圆由



求一个区域的体积
在我们的例子中,这是:
问题8:如何查找区域的体积
用圆柱盘的方法,求出图的区域的体积
围绕着
![[0,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/371602/gif.latex)





体积的公式为
在哪里
因此,

在求积分的时候,我们会用到幂逆法则,

应用这个规则我们得到

根据微积分第一基本定理的推论,
![\pi\left(\frac{1}{5}x^5\right)\left.\begin{matrix} \, \end{matrix}\right|_{0}^{10}=\pi \left(\left[\frac{1}{5}(10)^5\right]-\left[\frac{1}{5}(0)^5\right]\right)=20000\pi](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/373154/gif.latex)
因此,体积是

问题9:如何查找区域的体积
用圆柱盘的方法,求出图的区域的体积
围绕着
![[0,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/371603/gif.latex)





体积的公式为
在哪里
因此,

在求积分的时候,我们会用到幂逆法则,

应用这个规则我们得到

根据微积分第一基本定理的推论,
![\pi\left(\frac{1}{2}x^2\right)\left.\begin{matrix} \, \end{matrix}\right|_{0}^{3}= \pi\left(\left[\frac{1}{2}(3)^2\right]-\left[\frac{1}{2}(0)^2\right]\right)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/373158/gif.latex)
因此,体积是

问题1:体积
求旋转形成的固体形状的体积

![[0,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385876/gif.latex)
求在间隔上绕x轴旋转f(x)得到的立体体积
回想一下下面的固体体积公式:
其中A(x)等于旋转函数形成的圆盘的面积:
所以我们需要把它们放在一起:
那么,我们知道积分的极限一定是0和3,因为它们是我们要处理的区间。
(注意,代入0会得到0,所以我们只需要担心3)
所以我们的答案是:




















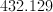


















![V = \int_0^1 \pi ~z~ dz = \pi \left[ \frac{z^2}{2} \right ]_0^1 = \pi \left( \frac{1}{2} - 0 \right ) = \frac{\pi}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/134552/gif.latex)


















![V=\pi\left[\frac{x^3}{3}-\frac{x^5}{5}\right]_{0}^{1}=\pi\left[\frac{1}{3}-\frac{1}{5}\right] = \frac{2\pi}{15}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/364927/gif.latex)








![V =\pi \left[x-\frac{1}{3}x^3\right]_{-\sqrt{2}/2}^{\sqrt{2}/2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/351943/gif.latex)















![[0,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/385877/gif.latex)












