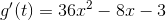现在就打电话安排辅导:

(888) 888 - 0446

AP微积分AB:的增减行为与的符号之间的关系

学习AP微积分AB的概念、例题和解释

创建帐户制作测试和抽认卡

所有AP微积分AB资源

3诊断测试 164实践测试今日问题抽认卡从概念中学习

例子问题

←之前 1 2 3. 4 5 下一个→

例子问题1:的增减行为与符号的关系

在哪个区间(s)是函数 f(x)=x^3+5x^2-8x+7 递增，在哪个(s)个区间递减?

可能的答案:

减少: $(-\infty ,-4), (\frac{2}{3},\infty)$

增加: $(-4,\frac{2}{3})$

增加: $(-\infty ,-4), (\frac{2}{3},\infty)$

减少: $(-4,\frac{2}{3})$

增加: $(-\infty,\infty)$

减少: $(-\infty,\infty)$

增加: $(-\infty,\frac{-2}{3}), (4,\infty)$

减少: $(\frac{-2}{3},4)$

正确答案:

增加: $(-\infty ,-4), (\frac{2}{3},\infty)$

减少: $(-4,\frac{2}{3})$

解释：

首先，我们必须通过设定法求出临界点 f'(x) 等于零。

f'(x)=0=3x^2+10x-8

然后反箔就得到

$0=(3x-2)(x+4)\Rightarrow 3x-2=0 \and\ x+4=0$

$x=\frac{2}{3}, x=-4$

这些是临界点。我们现在必须测试由临界点定义的每个区间上的值，以确定的符号 f'(x) 在每个间隔。

我们要检查的间隔是

$(-\infty,-4),(-4,\frac{2}{3}),(\frac{2}{3},\infty)$

我们有很多选择，但让我们选择吧 $x=-5, \ x=0 ,\ x=1$

$f'(-5)=3\cdot (-5^2)+10\cdot(-5)-8=17$

$f'(0)=3\cdot0^2 +10\cdot0-8=-8$

$f'(1)=3\cdot (1^2)+10\cdot (1)-8=5$

在第一个区间 f'(x) 是积极的意思 f(x) 正在增加。

在第二个区间 f'(x) 是消极的意思 f(x) 是减少的。

在第三个音程中 f'(x) 是积极的意思 f(x) 正在增加。

报告错误

例子问题2:的增减行为与符号的关系

关于函数是递增还是递减，一阶导数的符号告诉我们什么?

可能的答案:

一阶导数的符号并不能告诉我们函数是递增还是递减。

如果一阶导数是负的，那么函数是递减的。如果一阶导数是正的，那么函数是递增的。

如果一阶导数是正的，那么函数是递减的。如果一阶导数是负的，那么函数是递增的。

如果一阶导数为负，则函数递减，但如果一阶导数为正，则函数既不递增也不递减。

正确答案:

如果一阶导数是负的，那么函数是递减的。如果一阶导数是正的，那么函数是递增的。

解释：

关于函数是递增还是递减，一阶导数的符号告诉我们什么?

一阶导数检验用于判断函数在某一点或区间上是递增还是递减。

要使用这个检验，首先要找到函数的导数。然后，代入点的值，看看值上有什么符号。

如果一阶导数是负的，那么函数是递减的。如果一阶导数是正的，原始函数是递增的。如果一阶导数是0，那么原函数就有一个拐点。

报告错误

例子321:衍生品

使用一阶导数检验来判断当c=24时f(c)是增加还是减少。

f(c)=134c^2-325c+15

可能的答案:

递减，因为一阶导数是正的。

递减，因为一阶导数是负的。

递增，因为一阶导数是负的。

递增，因为一阶导数是正的。

正确答案:

递增，因为一阶导数是正的。

解释：

使用一阶导数检验来判断当c=24时f(c)是增加还是减少

f(c)=134c^2-325c+15

首先求f(c)的一阶导数

f'(c)=(2)134c-325=168c-325

接下来，代入24，求一阶导数的符号。

f'(24)=268(24)-325=6107

现在，一阶导数是正的，所以原函数一定是递增的。

报告错误

问题4:的增减行为与符号的关系

求g(t)的导数，判断g(t)在区间上是增加还是减少[5,6]。

g(t)=-12x^3+4x^2+3x

可能的答案:

g'(t)=36x^2-8x-3

增加

g'(t)=36x^2-32x-3

减少

g'(t)=-36x^2+32x+3

增加

g'(t)=-36x^2+8x+3

减少

正确答案:

g'(t)=-36x^2+8x+3

减少

解释：

求g(t)的导数，并判断g(t)在区间上是增加还是减少[5,6]

g(t)=-12x^3+4x^2+3x

首先，通过将每个指数减去1并将系数乘以该数字来求导数。

g'(t)=-(3)12x^2+2(4)x+3=-36x^2+8x+3

接下来，代入区间的两个端点看看g'(t)的符号是什么。

g'(t)=-36x^2+8x+3

g'(5)=-36(5)^2+8(5)+3=-900+40+3=-857

g'(6)=-36(6)^2+8(6)+3=-1296+48+3=-1245

显然这两个点都是负的，它们之间的每一点都是负的。这意味着函数g(t)在这个区间上是递减的。

报告错误

例5:的增减行为与符号的关系

判断f是增加还是减少．你怎么知道?

f(x)=14x^6-3x^5-137x^3+26x^2-12x-20

可能的答案:

F (x)是递增的，因为 f'(-12)<0

F (x)是递增的，因为 f'(-12)> 0

F (x)是递减的，因为 f'(-12)> 0

F (x)是递减的，因为 f'(-12)<0

正确答案:

F (x)是递减的，因为 f'(-12)<0

解释：

判断f是增加还是减少．你怎么知道?

f(x)=14x^6-3x^5-137x^3+26x^2-12x-20

为了检验是否增加/减少，我们需要找到一阶导数。

在这种情况下，我们可以用幂法则来做所有的微分。

权力规则:

$\frac{d}{dx}x^n=(n)x^{n-1}$

为了求一阶导数和二阶导数，我们每一项都要用到它。

对于每一项，我们将指数减去1，然后乘以原来的指数。

f(x)=14x^6-3x^5-137x^3+26x^2-12x-20

f'(x)=(6)14x^5-(5)3x^4-(3)137x^2+(2)26x-12

f'(x)=84x^5-15x^4-411x^2+52x-12

现在，我们需要找出f'(-12)的符号。这将告诉我们它是增加还是减少。

f'(-12)=84(-12)^5-15(-12)^4-411(-12)^2+52(-12)-12

f'(-12)=-20901890-311040-59184-624-12=-21,272,750

那么，我们得到

f'(-12)=-21,272,750

所以,

F (x)是递减的，因为 f'(-12)<0

报告错误

例子问题6:的增减行为与符号的关系

确定f在其整个定义域上递减的区间:

f=x^4+2x^3

可能的答案:

(-6, 0)

函数永不递减

$(-\infty, \infty)$

$(-\infty, -6)$

$(-6, \infty)$

正确答案:

$(-\infty, -6)$

解释：

为了确定函数递减的区间，我们必须确定函数一阶导数为负的区间。

函数的一阶导数等于

f'=x^3+6x^2

并被发现使用以下规则:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

接下来，我们必须找到临界值，在这个临界值下，一阶导数等于零:

x^3+6x^2=0

x^2(x+6)=0

c=-6, 0

使用临界值，我们现在创建一个区间来计算一阶导数的符号:

$(-\infty, -6), (-6,0), (0, \infty)$

注意在区间的边界上，一阶导数既不是正的也不是负的。

在第一个区间上，一阶导数为负，而在其余区间上，一阶导数为正。因此，函数在第一个区间上递减， $(-\infty, -6)$ ．

报告错误

示例问题7:的增减行为与符号的关系

确定f递减的区间:

$f=x^5+\frac{x^3}{3}$

可能的答案:

函数永不递减

$(-\infty, \infty)$

$(-\infty, 0)$

$(0, \infty)$

正确答案:

函数永不递减

解释：

为了确定函数递减的区间，我们必须确定函数一阶导数为负的区间。

函数的一阶导数等于

f'=5x^4+x^2

并被发现使用以下规则:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

接下来，我们必须找到临界值，在这个临界值下，一阶导数等于零:

5x^4+x^2=0

x^2(5x^2+1)=0

c= 0

负数的平方根对于临界值是无效的，所以这个函数只有一个临界值。

使用临界值，我们现在创建一个区间来计算一阶导数的符号:

$(-\infty, 0), (0, \infty)$

注意在区间的边界上，一阶导数既不是正的也不是负的。

在第一个区间，一阶导数是正的，在第二个区间，一阶导数也是正的。函数因此永不递减因为一阶导数永不为负。

报告错误

例8:的增减行为与符号的关系

确定f递增的区间:

$f=\cos(5x), 0\leq x \leq \frac{2\pi}{5}$

可能的答案:

$(\frac{\pi}{5}, \infty)$

$(0, 2\pi)$

$(\frac{\pi}{5}, \frac{2\pi}{5})$

函数是不递增的

$(\frac{\pi}{5}, \frac{2\pi}{5})$

正确答案:

$(\frac{\pi}{5}, \frac{2\pi}{5})$

解释：

为了确定函数递增的区间，我们必须确定函数一阶导数为正的区间。

函数的一阶导数等于

$f'=-5\sin(5x)$

并被发现使用以下规则:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ ， $\frac{\mathrm{d} }{\mathrm{d} x} \cos(x)=-\sin(x)$ ， $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

接下来，我们必须找到临界值，在这个临界值下，一阶导数等于零:

$-5\sin(5x)=0$

$c=0, \frac{\pi}{5}, \frac{2\pi}{5}$

请注意，我们不再根据问题语句中的给定间隔编写临界值。

使用临界值，我们现在创建一个区间来计算一阶导数的符号:

$(0, \frac{\pi}{5}), (\frac{\pi}{5}, \frac{2\pi}{5})$

注意在区间的边界上，一阶导数既不是正的也不是负的。

通过将给定区间上的任意值代入一阶导数函数来计算符号，我们发现在第一个区间上，一阶导数为负，而在第二个区间上，一阶导数为正。因此，函数在第二个区间上递增， $(\frac{\pi}{5}, \frac{2\pi}{5})$ ．

报告错误

问题9:的增减行为与符号的关系

确定以下函数的局部极小值:

f=-x^3+2

可能的答案:

x=0

$x=\infty$

x=-3

该函数没有局部最小值

正确答案:

该函数没有局部最小值

解释：

为了确定函数的局部极小值，我们必须确定函数的一阶导数从负变为正的点。

函数的一阶导数是

f'=-x^3+2

并被发现使用以下规则:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

接下来，我们必须找到临界值，在这个临界值下，一阶导数等于零:

-3x^2=0

c=0

使用临界值作为端点，我们现在创建一个区间来计算一阶导数的符号:

$(-\infty, 0), (0, \infty)$

注意在区间的边界上，一阶导数既不是正的也不是负的。

通过将给定区间上的任意值代入一阶导数函数来计算符号，我们发现在第一个区间上，一阶导数为负，在第二个区间上，一阶导数也是负的。一阶导数在符号上从不从负到正变化，因此函数不存在局部极小值。

报告错误

例子问题10:的增减行为与符号的关系

求下列函数的局部极大值:

$f= \frac{x^3}{3}+x^2+x$

可能的答案:

x=1

不存在局部极大值

$x=\infty$

x=0

x=-1

正确答案:

不存在局部极大值

解释：

为了确定函数的局部极大值，我们必须确定函数的一阶导数从正变为负的点。

函数的一阶导数是

f'=x^2+2x+1

并被发现使用以下规则:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ ， $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

接下来，我们必须找到临界值，在这个临界值下，一阶导数等于零:

x^2+2x+1=(x+1)^2=0

c=-1

使用临界值作为端点，我们现在创建一个区间来计算一阶导数的符号:

$(-\infty, -1), (-1, \infty)$

注意在区间的边界上，一阶导数既不是正的也不是负的。

通过将给定区间上的任意值代入一阶导数函数来求符号，我们发现在第一个区间上，一阶导数是正的，在第二个区间上，一阶导数也是正的。一阶导数没有符号变化，因此不存在局部极大值(函数总是递增)。

报告错误

←之前 1 2 3. 4 5 下一个→

查看AP微积分AB导师

两代情
认证导师

纽约哥伦比亚大学，文学学士，政治学和政治学。

查看AP微积分AB导师

埃文
认证导师

密歇根大学安娜堡分校，文学学士，犹太研究。

查看AP微积分AB导师

赞恩
认证导师

内华达大学雷诺分校，机械工程学士。范德比尔特，生物医学工程硕士。

所有AP微积分AB资源

3诊断测试 164实践测试今日问题抽认卡从概念中学习

受欢迎的科目

旧金山湾区的阅读导师，休斯顿的GMAT家教，华盛顿特区的MCAT导师，ISEE导师在华盛顿特区，波士顿的SAT辅导老师，华盛顿特区的西班牙语导师，旧金山湾区MCAT导师，洛杉矶的LSAT导师，波士顿的微积分导师，旧金山湾区的LSAT辅导老师

常用备考

波士顿MCAT考试准备，ISEE考试准备在圣地亚哥，在丹佛准备GRE考试，在纽约准备GMAT考试，洛杉矶的LSAT考试准备，ISEE考试准备在芝加哥，在达拉斯沃斯堡的SSAT考试准备，在西雅图准备SSAT考试，费城ISEE考试准备中心，在旧金山湾区的MCAT考试准备

DMCA的抱怨

如果您认为通过本网站提供的内容(定义见我们的服务条款)侵犯了您的一项或多项版权，请通过向下列指定代理提供包含以下信息的书面通知(“侵权通知”)通知我们。如果校队导师对侵权通知采取行动，它将通过该方提供给校队导师的最新电子邮件地址(如果有的话)，善意地尝试联系提供此类内容的一方。

您的侵权通知可能会转发给提供内容的一方或ChillingEffects.org等第三方。

请注意，如果您严重歪曲某产品或活动侵犯了您的版权，您将承担损害赔偿(包括诉讼费和律师费)。因此，如果您不确定网站上的内容或网站链接的内容侵犯了您的版权，您应该首先考虑联系律师。

请按照以下步骤提交通知:

你必须包括以下内容:

版权所有人或授权代表其行事的人的实物或电子签名;声称被侵犯的版权的证明;对您声称侵犯您版权的内容的性质和确切位置的描述，足够详细，以允许大学导师找到并积极识别该内容;例如，我们需要一个特定问题的链接(不仅仅是问题的名称)，其中包含内容和问题的具体部分的描述-图像，链接，文本等-您的投诉指的是;你的姓名、地址、电话号码及电邮地址;您的声明:(A)您真诚地相信，您声称侵犯您版权的内容的使用未经法律或版权所有者或该所有者的代理人授权;(b)您的侵权通知中包含的所有信息都是准确的，并且(c)在伪证罪的处罚下，您是版权所有人或被授权代表他们行事的人。

将投诉发送给我们的指定代理人:

Charles Cohn Varsity Tutors LLC
汉利路101号，300室
圣路易斯，密苏里州63105

或者填写下面的表格:

不填写这个字段吗

联系信息

＊法定全称

公司名称

＊电话号码

＊电子邮件地址

地址

＊Address1

Address2

＊城市

＊状态

＊Zipcode

＊国家

投诉细节

您所代表的版权方(如果不是您本人)

＊版权作品的URL(您的原始材料所在的位置)

＊请描述受版权保护的作品，以便于识别

我是所有权人，或者是被授权代表被侵犯的专有权的所有者行事的代理人。

这个通知是准确的。

我承认，使用此程序提出虚假或恶意侵犯版权的指控可能会产生不利的法律后果。

＊签名(您的数字签名具有法律约束力)

高中

研究生院

学习

搜索50+测试

数学辅导

科学辅导

外语

小学辅导

其他

搜索350多个主题

AP微积分AB:的增减行为与的符号之间的关系

学习AP微积分AB的概念、例题和解释

所有AP微积分AB资源

例子问题

例子问题1:的增减行为与符号的关系

例子问题2:的增减行为与符号的关系

例子321:衍生品

问题4:的增减行为与符号的关系

例5:的增减行为与符号的关系

例子问题6:的增减行为与符号的关系

示例问题7:的增减行为与符号的关系

例8:的增减行为与符号的关系

问题9:的增减行为与符号的关系

例子问题10:的增减行为与符号的关系

所有AP微积分AB资源

报告与此问题有关的问题

DMCA的抱怨

联系信息

地址

投诉细节

找到最好的导师

电子邮件地址:
你的名字:

电子邮件地址:
你的名字:
反馈: