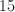例子问题
例子问题2:如何找到角度的度量
两个角互为补角,比例为1:4。小一点的角的大小是多少?
因为这两个角互为补角,所以它们的和是180度。因为它们的比例是1:4,所以表达式可以写成:
例子问题1:几何

AB和CD是两条平行线,与直线EF相交。如果角1的度数是
角是相等的。当两条平行线与一条截线相交时,它们的同位角具有相同的度量。
例子问题1:相交线与角
非按比例绘制的图形。
在上图中,APB形成一条直线。如果角APC比角DPB大81度,且角CPD和角DPB相等,那么角CPB的度数是多少?
33
114
66
40
50
66
令x等于角DPB的长度。因为角APC的度数比角DPB的度数大81度,所以我们可以把这个角的度数表示为x + 81。同样,因为角CPD的长度等于角DPB的长度,我们可以用x来表示CPD的长度。
由于APB是一条直线,所以角DPB、角APC和角CPD的度数之和必须都等于180;因此,我们可以写出下面的方程来求x:
X + (X + 81) + X = 180
通过收集x项来简化。
3x + 81 = 180
两边同时减去81。
3x = 99
除以3。
X = 33。
这意味着角DPB和角CPD的度数都等于33度。最初的问题要求我们求角CPB的度数,它等于角DPB和角CPD的度数之和。
测量CPB = 33 + 33 = 66。
答案是66。
例子问题1:相交线与角
角ABC补角的二分之一等于角ABC补角的两倍。角ABC的补角的度数是多少?
90
36
72
54
18
54
设x等于角ABC的角,设y等于角ABC的补角,设z等于角ABC的补角。
因为x和y是互补的,所以它们的值之和必须等于180。换句话说,x + y = 180。
我们被告知,补充品的一半等于ABC的两倍。我们可以把这个方程写成这样:
(1/2)y = 2x。
因为x + y = 180,我们可以用x来表示y两边同时减去x。换句话说,y = 180 - x。接下来,我们可以把这个值代入方程(1/2)y = 2x,然后解出x。
(1/2)(180-x) = 2x。
两边同时乘以2,就消去了分数。
(180 - x) = 4x。
两边同时加上x。
180 = 5倍。
两边同时除以5。
X = 36。
角ABC的度数是36度。然而,原来的问题要求我们求ABC的补角的度数,我们之前记为z。因为一个角的度数与其补角的度数之和等于90,所以我们可以写出下面的方程:
X + z = 90。
现在,我们可以把36代入x的值,然后解出z。
36 + z = 90。
两边同时减去36。
Z = 54。
答案是54。
例子问题1:平面几何

图中AB || CD. a+b的值是多少?
160°
其他答案都没有。
140°
80°
60°
160°
阅读说明时请参考下图:

我们知道角b必须等于它的对顶角(直接“穿过”交点的角)。因此,它是20°。
此外,根据平行线的性质,我们知道a的补角一定是40°。根据补充法则,我们知道a + 40°= 180°。求a,得到a = 140°。
因此,a + b = 140°+ 20°= 160°
例子问题1:如何求两条线的夹角
在矩形ABCD,两条对角线均画出并相交于一点E.
让测量角度AEB平等的x度。
让测量角度BEC平等的y度。
让测量角度清洁能源平等的z度。
求角度的度数AED在这方面x,y和/或z.
180 -y
180 - 2(x+z)
180 - (x+y+z)
360 -x+y+z
180 - 1/2(x+z)
180 - 1/2(x+z)
相交线形成两对相等的对顶角。因此,我们可以推导出y角度测量AED.
而且,相交的直线会形成互补的邻角(和为180度)。因此,我们可以推导出x+y+z+(角度测量AED) = 360。
把第一个方程代入第二个方程,得到
x+(角度测量AED) +z+(角度测量AED) = 360
2(测量角度AED) +x+z= 360
2(测量角度AED) = 360 - (x+z)
除以2得到:
角度测量AED= 180 - 1/2(x+z)
例子问题2:平面几何
一个学生给他的朋友制造了一个挑战。他首先画了一个正方形,然后为每条对角线加上一条直线。最后,他让他的朋友画一个交点最多的圆。
这个圆有多少个交点?

例子问题2:平面几何
两对平行线相交:

如果A = 135o2*|B-C| =多少?
170°
140°
180°
150°
160°
180°
根据平行线A+B = 180的性质o, b = 45o, c = a = 135o,所以2*|B-C| = 2*| 45-135| = 180o
例子问题2:几何
行





信息不够。
因为我们知道对角相等,所以它遵循这个角

想象一条平行线穿过一点




例子问题1:几何
如果


当一个角的度数与它的补充度数相加时,结果总是180度。换句话说,如果两个角的度数之和为180度,则两个角互为补角。例如,两个角的度数分别为50度和130度,它们互为补角,因为50度和130度的和是180度。因此,我们可以写出下面的方程:
两边同时减去40。
添加
答案是